Think About Angles
Opening
Think About Angles
- Describe the angle(s) in this figure.
- Discuss your ideas with your class.



Discuss the following with your classmates.

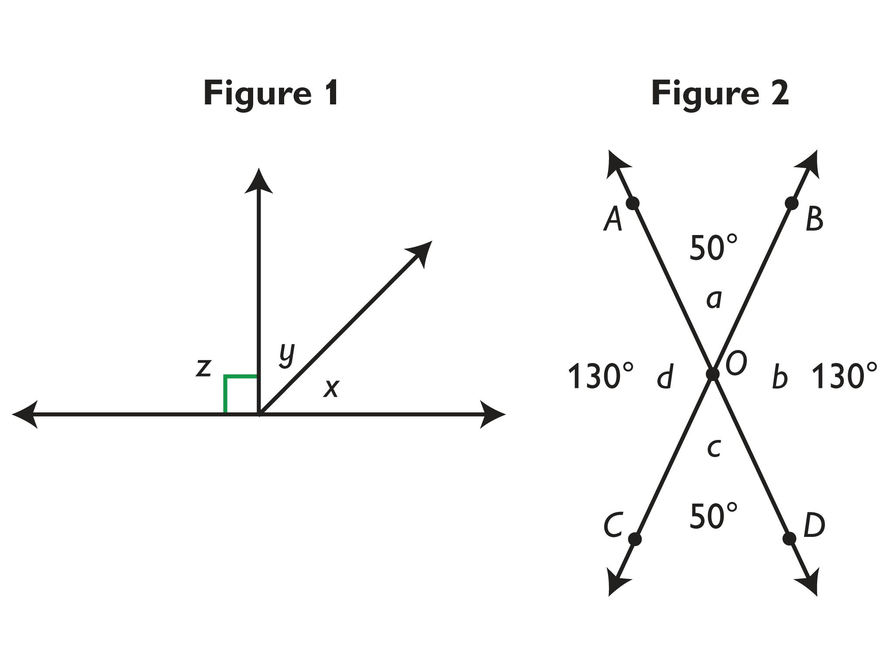
Explore the relationships between adjacent, supplementary, complementary, and vertical angles.

Use the Angles Sketch interactive to explore each set of angles:
Answer the following questions.
INTERACTIVE: Angles Sketch
Try adding different angles together. What is their sum? Which angles are congruent?
Summarize the observations you made about angle relationships and the sums of angles.
Take notes about your classmates’ observations concerning angle relationships and the sum of angles.
As your classmates present, ask questions such as:
Read and Discuss
Can you:
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I think complementary and supplementary angles are similar in these ways… and different in these ways …