Angles in a Triangle
Opening
Angles in a Triangle
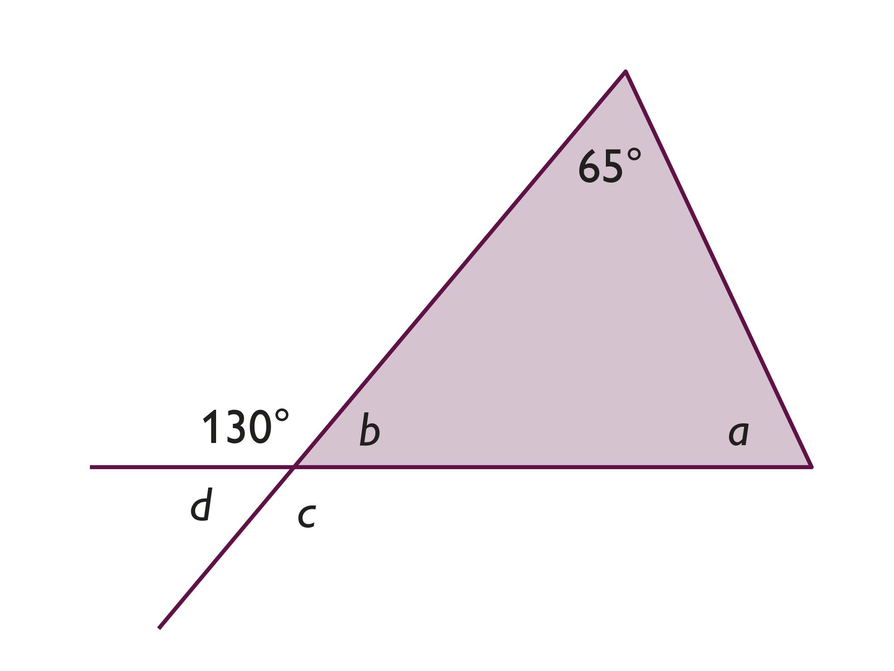
Look at this triangle.
- What do you know about the angles in this triangle?
- Can you use what you know to solve for x?


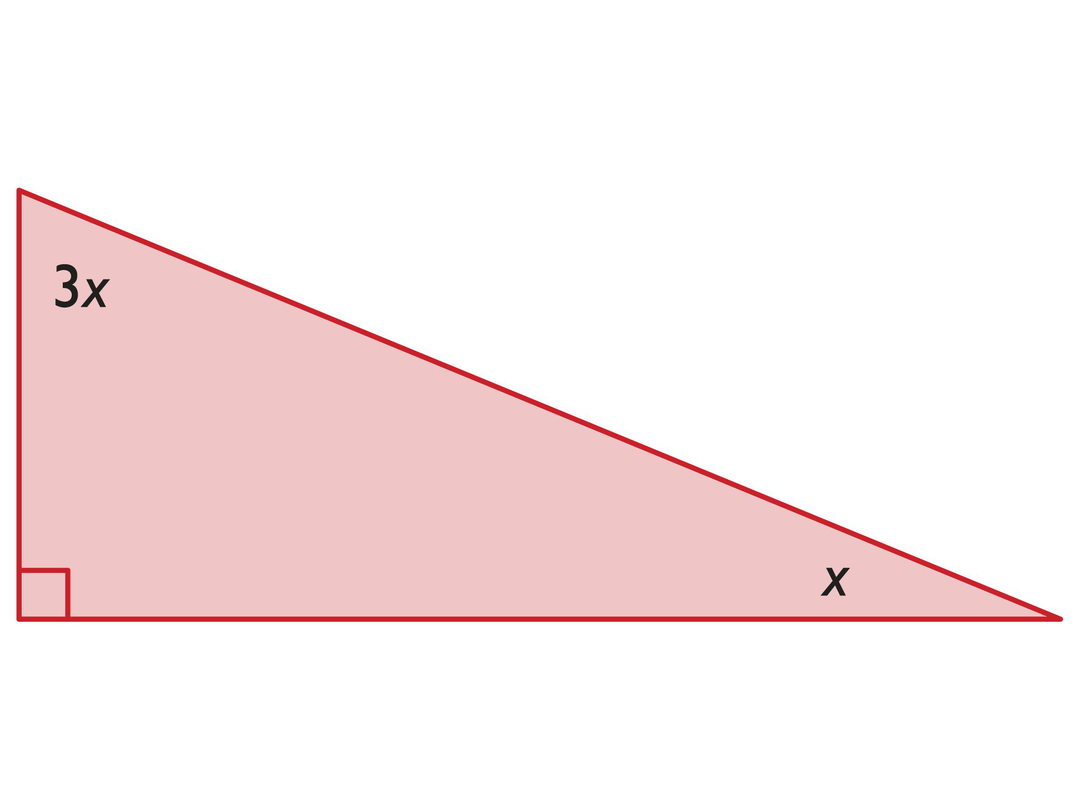
Look at this triangle.

Use your knowledge of geometric figures to determine missing angle measures in polygons.
This quadrilateral is a parallelogram.

This quadrilateral is a rhombus.


This figure is a regular pentagon.

What do you know about the angles in a regular pentagon?
Take notes about your classmates' strategies and explanations for finding the missing angle measures.
As your classmates present, ask questions such as:
Write a summary about finding missing angle measures in polygons.
Check your summary:
Complete this Self Check by yourself.
The large figure is a hexagon. Figures ABGF andCDEF are parallelograms.

Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
When I look at triangles, quadrilaterals, and other polygons, I see these connections …