Funciones Seccionadas
Funciones Seccionadas
“Las funciones seccionadas son aquellas que están compuestas por funciones individuales, cuando se agrupan en una sola función, da como resultado una función seccionada.”
Ejemplo:
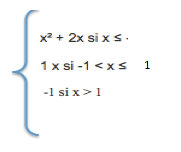
Proceso
Si vemos el ejemplo anterior, y tomamos la primera función, podemos ver que tiene una restricción en la cual x debe ser menor o igual a menos uno (x ≤ -1).
Como debe ser menor o igual a menos uno, tomamos este número como base para empezar a tabular y posteriormente, realizar la gráfica.
| x | y |
| -1 | -1 |
| -2 | 0 |
| -3 | 3 |
¿Cómo se obtuvieron estos resultados? Simplemente escogemos valores para x, que cumplan la restricción que se indica en la función. En este caso, lo números menores o iguales a uno la cumplen, por lo que por eso se eligieron el -1, -2 y -3.
Ya que tenemos los valores de x, debemos sacar los valores de y. Para esto utilizaremos los valores de x que ya tenemos y los utilizaremos para sustituir la x de nuestra función inicial.
(-1) ² + 2 (-1) = -1
(-2) ² + 2 (-2) = 0
(-3) ² + 2 (-3) = 3
Ya que tenemos la primera función, será necesario hacer lo mismo con las que faltan.
f (x) = { x si -1 < x ≤ 1}
| x | y |
| -1 | -1 |
| 1 | 1 |
f (x) = {-1 si x > 1}
| x | y |
| 1 | -1 |
| 2 | -1 |
| 3 | -1 |
Se puede ver que, por ejemplo, en la última función, los valores de x debían ser mayores a uno, por lo que el uno no entraba en la tabulación, ¿cierto?. Lo que sucede aquí es que es necesario colocar los números que nos restringen la función, por que son esenciales para su gratificación.
Para graficar esta función seccionada, vamos a ocupar todas las tabulaciones anteriormente realizadas.
(Nota: Para ayudarte a graficar, puedes utilizar GeoGebra, un sitio de internet gratis, en el cual puedes trazar todo tipo de funciones. https://www.geogebra.org/m/352279 )

Como podemos observar en la gráfica, existen dos tipos de puntos, los puntos abiertos y los puntos cerrados. Estos puntos nos ayudarán a sacar el dominio y el rango de nuestra función.
Viendo nuestra restricciones, podemos saber si nuestros puntos serán cerrados o abiertos. Por ejemplo:
El punto será cerrado, ya que es menor o igual a -1.
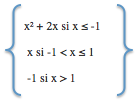
El primer punto será abierto y el segundo será cerrado.
El punto cero abierto, ya que x es mayor a 1.
Si los signos son: ≥ o ≤ , el punto siempre será cerrado.
Si los signos son > o < , el punto será abierto.
En el caso de la segunda función, el punto debería de ser abierto, pero como es el punto de unión entre un punto cerrado y uno abierto, el punto cerrado vence y ese es el que se marca.
Dominio y Rango
Para poder sacar el dominio y el rango de todas las funciones, es necesario saber algunos puntos básicos:
∞: Significa infinito, es decir, todos los números positivos. El -∞ significan todos los números negativos.
∈ : Significa perteneciente, o pertenece a.
Los corchetes [ ], es la forma escrita de poner los puntos cerrados, es decir los mayores/menores o iguales a. (≥ o ≤ )
Los paréntesis ( ) , son la forma de escribir los puntos abiertos de las gráficas, es decir, los > o <.
El dominio de la función, son todos los valores que x puede tomar. En este caso sería:
D f(x): x ∈ R o (-∞, ∞ )
Este es el dominio ya que tanto nuestra parábola, como nuestra recta de la función 3, son infinitas, por lo que nuestros valores de x, no tienen un fin especificado.
El rango son todos los valores que puede tomar y, en este caso es necesario observar la gráfica para poder sacarlo más rápidamente. Para sacar el rango, imaginemos que tenemos una regla de forma horizontal, y queremos saber a partir de qué valor de y, empieza nuestra gráfica. La regla irá subiendo, es decir, empieza desde abajo hasta encontrar el primer punto en donde esté y marcado.
En esta gráfica, nuestra regla pararía en el -1, que es el primer punto que aparece en nuestra gráfica donde y está marcado. Por lo tanto, nuestro rango sería:
R f(x): [-1, ∞)
Nuestro rango es de menos uno (corchete, ya que es punto cerrado) a infinito, ya que nuestra parábola no tiene un fin especificado.
EJERCICIOS
1a Parte
Determina el dominio y el rango según la gráfica
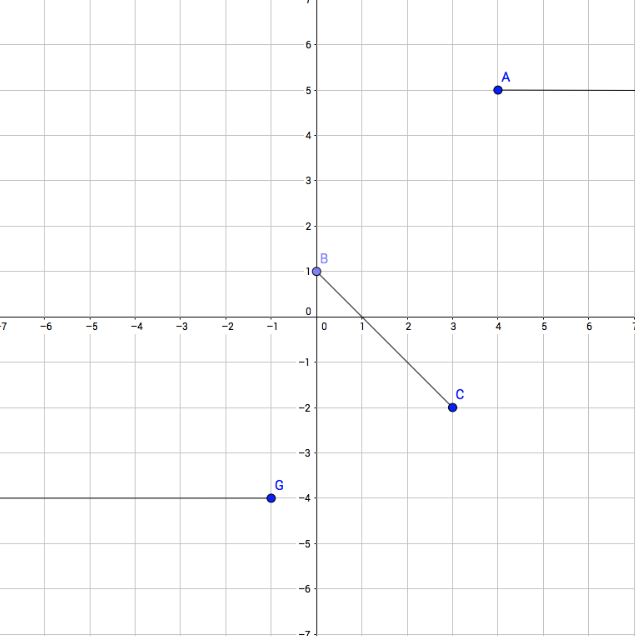
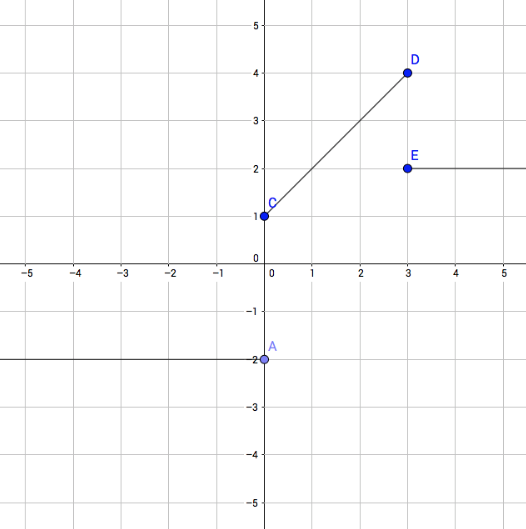
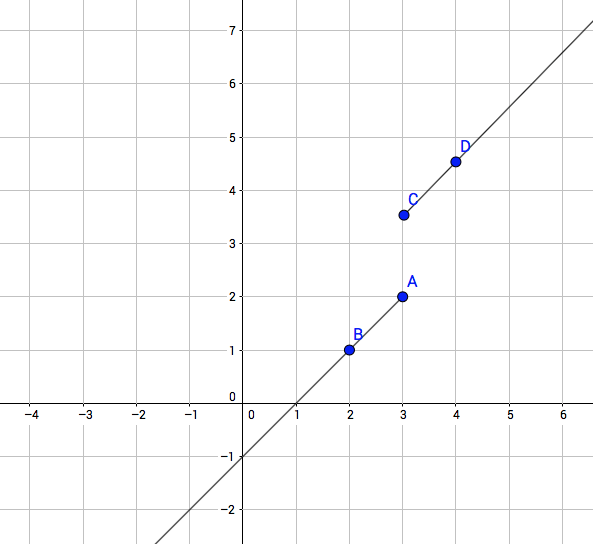
2a Parte
Grafica las siguientes funciones seccionadas y determina su dominio y su rango.
A)
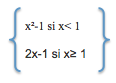
B)
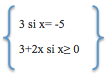
C)
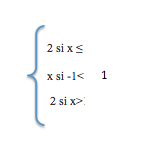
Evaluación
Respuestas
Respuestas de función seccionada
Fuentes
http://www.vitutor.com/fun/2/c_11.html
http://www.sangakoo.com/es/temas/funciones-definidas-a-trozos
http://cursos.tecmilenio.edu.mx/cursos/at8q3ozr5p/prepa/pm/pm09022/anexos/explica13.htm