Algebra Toothpick Patterns
Lesson Goals
The students will recognize and extend growing patterns and be able to develop a verbal or written rule which generalizes the pattern. Students will be able to generate and organize data.
The Task - Toothpick Patterns
- Create the following toothpick pattern with the stack of toothpicks you have been given. Record how many toothpicks it takes to create each figure and record the information in your table.
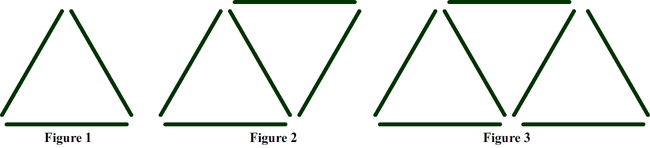
2. Follow the pattern and create the next 3 figures using your toothpicks, and fill in your table with the number of toothpicks needed for each figure.
3. Draw the six figures on your paper so you have a drawing of the pattern.
4. Now see if you can jump to the 10th figure without drawing or creating the figures in between. Create and draw the 10th figure in the pattern without creating figures 7,8,9, and 10.
5. Try to develop a rule that would allow you to calculate the number of toothpicks needed for any figure any the pattern. For example, how many toothpicks would you need for the 1000th figure in the pattern.
Perimeter
Now let's look at the perimeter of the toothpick figures. For this pattern we will not count the toothpicks in the interior of each figure.
- Record the perimeter of each figure in your table.
- Develop a rule to determine the number of toothpicks in the perimeter of any figure in that pattern. For example, how many toothpicks are there in the perimeter of the 1000th figure?
- Compare the two patterns. What is the same and what is different?
Possible Solution Strategies
- Students may use toothpicks to extend the pattern.
- Students may draw the next figures in the pattern.
- Students may develop a numeric pattern to determine the number of toothpicks in the next figure.
- Students may develop a function to determine the number of toothpicks in any
Students Misconceptions and Potential Difficulties
- Students may have a limited understanding of growing patterns, thinking the pattern simply repeats. For example, 2,4,6 (the pattern is add two), some students may just repeat, 2,4,6,2,4,6,2,4,6 etc.
- Students may have difficulty seeing the connection from one figure of the pattern to the next.
- Students may have difficulty determining the algebraic expressions that determine the number of toothpicks in any figure.
- Students may recognize the growth pattern, but have difficulty translating their thoughts verbally or into an algebraic expression.
- Students may complete the chart incorrectly.
- Students my determine an incorrect rule.
- Student my find a pattern different from the expected or typical pattern.
Strategies for Clarifying Misconceptions and Potential Difficulties
- Using toothpicks will help make the pattern more concrete for some learners.
- Giving students a chart will provide scaffolding that some students may need.
- Classroom discussion can help flush out the pattern rules.