WP.2.6 ADDITIONAL MEASURES OF LOCATION PROBLEMS (INCLUDING MS EXCEL)

[WP.2.6]

WHITE PAPER TOPIC: ADDITIONAL MEASURES OF LOCATION PROBLEMS (INCLUDING MS EXCEL)

I.               ADDITIONAL EXERCISES

[Formula Note]

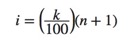
Interval Calculation Formula

 (Use for Problems 1-8) For the following; set of 20 data points:

[Ref. H.63 OER Data Set]

Problem 1:  What is first quartile value?

Problem 2:  What is the Median value?

Problem 3:  What is third quartile value?

Problem 4:  What is the calculated IQR?

Problem 5 What is 33 percentile value?

Problem 6: What is 80 percentile value?

Problem 7:  What is 57 percentile value?

Problem 8:  What is 95 percentile value?

(Use for Problems 9-16) For the following; set of data:

Problem 9:  What is first quartile value?

Problem 10:  What is the Median value?

Problem 11:  What is third quartile value?

Problem 12:  What is the calculated IQR?

Problem 13: What is 43 percentile value?

Problem 14: What is 70 percentile value?

Problem 15:  What is 77 percentile value?

Problem 16:  What is 93 percentile value?

(Use for Problems 17-24) For the following; set of data:

Problem 17:  What is first quartile value?

Problem 18:  What is the Median value?

Problem 19:  What is third quartile value?

Problem 20:  What is the calculated IQR?

Problem 21: What is 32 percentile value?

Problem 22: What is 65 percentile value?

Problem 23:  What is 41 percentile value?

Problem 24:  What is 68 percentile value?

SOLUTIONS:

Problem 1: 60.25                     L₂₅=(20+1)(25/100)=21*.25 = 5.25 {67-58 = 9} (.25*9=2.25) 58+2.25=60.25

Problem 2: 86.5                       L₅₀=(20+1)(50/100)=21*.50 = 10.5 {87-86=1} (.50*1=.5) 86+.5=86.5

Problem 3: 104.25                   L₇₅=(20+1)(75/100)=21*.75 = 15.75 {106-99=7} (.75*7=5.25) 99+5.25=104.25

Problem 4: 44                           104.25-60.25=44

Problem 5: 67.93                     L₃₃=(20+1)(33/100)=21*.33=6.93 67+.93=67.93

Problem 6: 110.8                     L₈₀=(20+1)(80/100)=21*.80=16.8 {112-106=6} (.80*6=4.8) 106+4.8=110.8

Problem 7: 94.76                     L₅₇=(20+1)(57/100)=21*.57=11.97 {95-87=8} (.97*8=7.76) 87+7.76=94.76

Problem 8: 149.75                   L₉₅=(20+1)(95/100)=21*.95=19.95 {150-145=5} (.95*5=4.75) 145+4.75=149.75

Problem 9: 68                          L₂₅=(36+1)(25/100)= 37*.25=9.25 {68-68=0} (.25*0=0) 68+0=68

Problem 10: 78.5                     L₅₀=(36+1)(50/100)=37*.50=18.5 {79-78=1} (.50*1=.5) 78+.5=78.5

Problem 11: 87                        L₇₅=(36+1)(75/100)= 37*.75=27.75 {87-87=0} (.75*0=0) 87+0=87

Problem 12: 19                        87-68=19

Problem 13: 72.91                  L₄₃=(36+1)(43/100)=37*.43=15.91  72+.91= 72.91

Problem 14: 85.8                    L₇₀=(36+1)(70/100)=37*.70=25.9 {86-84=2} (.9*2=1.8) 84+1.8=85.8

Problem 15: 87.49                  L₇₇=(36+1)(77/100)=37*.77=28.49 87+.49=87.49

Problem 16: 98.41                  L₉₃=(36+1)(93/100)=37*.93=34.41 98+.41=98.41

Problem 17: 1090                   L₂₅=(10+1)(25/100)=11*.25=2.75 {1100-1060=40} (.75*40=30) 1060+30=1090

Problem 18: 1850                   L₅₀=(10+1)(50/100)=11*.50=5.5 {1900-1800=100} (.50*100=50} 1800+50=1850

Problem 19: 2115                   L₇₅=(10+1)(75/100)=11*.75=8.25 {2160-2100=60} (.25*60=15} 2100+15=2115

Problem 20: 1025                   2115-1090=1025

Problem 21: 1165                   L₃₂=(10+1)(32/100)=11*.32=3.52 {1225-1100=125} (.52*125=65) 1100+65=1165

Problem 22: 2015                   L₆₅=(10+1)(65/100)=11*.65=7.15 2000+15=2015

Problem 23: 1518.25              L₄₁=(10+1)(41/100)=11*.41=4.51 {1800-1225=575} (.51*575=293.25) 1225+293.25=1518.25

Problem 24: 2048                   L₆₈=(10+1)(68/100)=11*.68=7.48 2000+48=2048

II. CALCULATING PERCENTILES IN MS EXCEL

Excel includes a function that will calculate percentiles given a set of data points and a desired percentile value. Our goal for this section is to calculate the 10^th percentile, 20^th percentile, 30^th percentile, and so forth up until the 90^th percentile, as well as the values for Q1 and Q3. Start by copying and pasting the following data into an Excel spreadsheet.

1.     Beginning in cell A6, type the following values into column A to serve as labels for each percentile value.

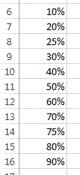
Excel Screenshot 1

2.     With cell B6 selected (relating to the 10th percentile), click on the Insert Function button (fx) and type in “Percentile”.

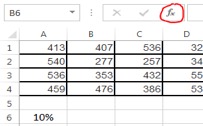
Excel Screen Shot 2

 3.     Select the option titled “PERCENTILE.EXC” and click OK.

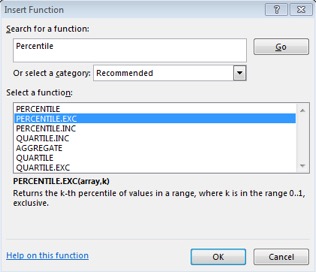
Excel Screen Shot 3

 4.     Within the function arguments, the array represents our raw data. With your mouse, select this data. An absolute reference is required for the array to ensure the same array is referenced when the formula is copied (press F4 after highlighting the array or fn+ F4 on some laptops). For K, click on the cell containing the percentile value (A6).

5.     The formula should output a value of 278.4 for the 10th percentile.

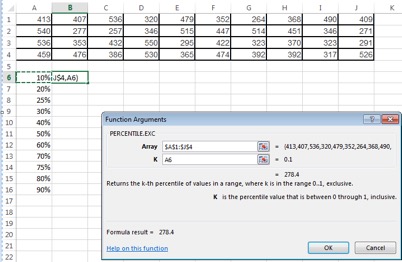
Excel Screen Shot 4

6.     Copy the formula down for the remaining percentile values.

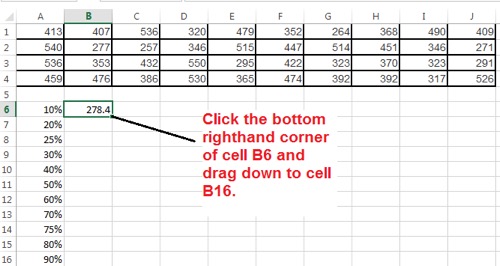
Excel Screen Shot 5

7.     The final results should match the following table.

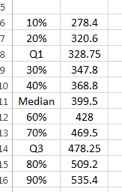
Excel Screen Shot 6