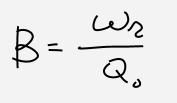RLC serie passabanda

RLC serie passabanda

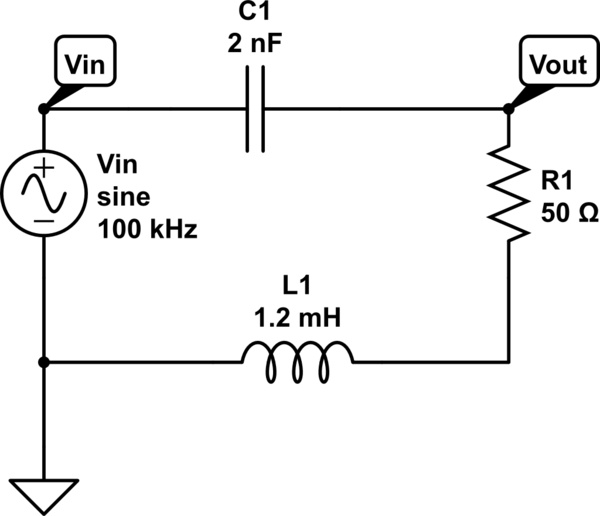
Simulazione disponibile qui: https://www.circuitlab.com/circuit/5c747w/rlc-serie-passa-banda/

Possiamo immaginare questo filtro come la serie di un passa alto ( il comportamento del condensatore) e di un passabasso (comportamento dovuto alla bobina). Dunque se l'uscita, come in figura, è prelevata sul resistore, il comportamento sarà quello di attenuare sia le basse che le alte frequenze.

Esisterà allora una frequenza alla quale la reattanza del condensatore sarà uguale e opposta alla reattanza della bobina. La chiameremo frequenza di risonanza.

E' facile osservarlo anche matematicamente a partire dalla espressione della impedenza vista dal generatore:

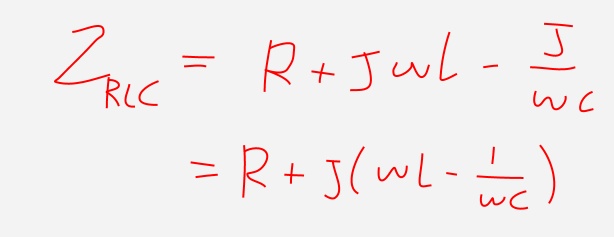
Notiamo il termine tra parentesi. Se lo poniamo pari a zero, ovvero ipotizziamo che le reattanze capacitive e induttive siano uguali, avremo:

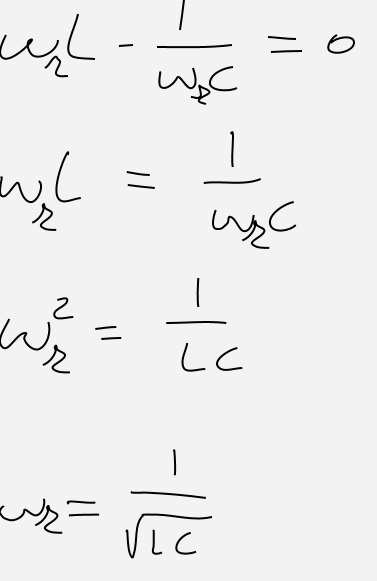
Di conseguenza la frequenza di risonanza fr si calcola in accordo alla seguente:

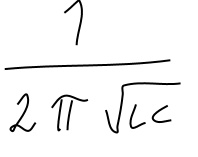
che,  con i valori dei componenti in figura vale poco più di 100kHz.

Infatti lanciando la simulazione otteniamo i seguenti diagrammi:

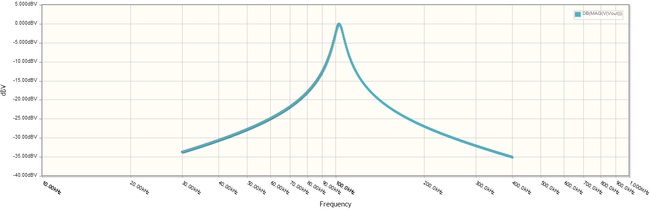
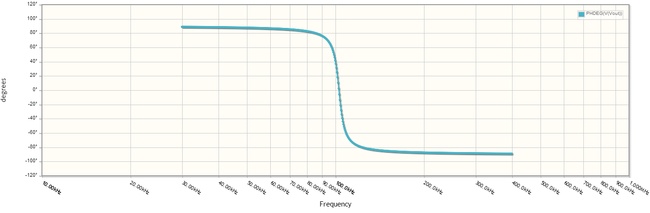
dai quali notiamo:

• il massimo della ampiezza la abbiamo proprio alla frequenza di risonanza
• la fase passa da -90° (comportamento capacitivo) a +90° (comportamento induttivo)
• alla frequenza di risonanza la fase è pari a zero (comportamento puramente resistivo).

Abbiamo ottenuto un filtro che taglia le frequenze al di sopra e al di sotto della frequenza di risonanza.

Molto indicativo del comportamento del filtro è il coefficiente di qualità:

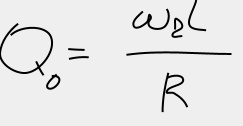
Nel caso appena visto: 

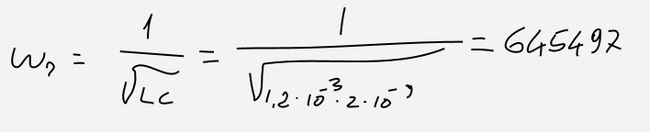
e 

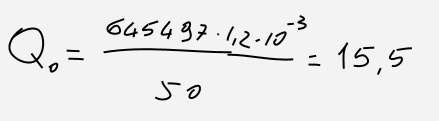
In queste condizioni diciamo che il filtro è molto selettivo, cioè consente il transito solo di un range molto piccolo di frequenze vicine a quella di risonanza.

Nel caso, invece, in cui sia Q0 < 0,5, per esempio con R = 5kohm la curva mostra una zona piatta, la "banda passante".

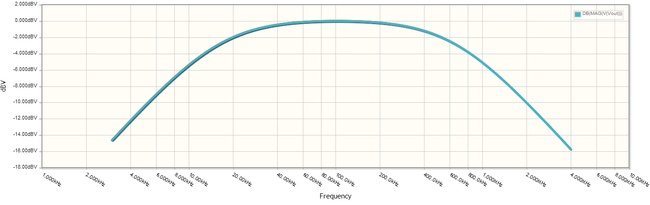
In questo caso la selettività del filtro è limitata ed abbiamo una banda passante  definita come la differenza tra la frequenza di taglio superiore e quella inferiore.

Dall'espressione della funzione di trasferimento ricaviamo ( qui non lo dimostriamo) che la banda passante B sarà: