Elettronica Digitale - Logica Combinatoria
Cosa è l'elettronica digitale
Dove si parla della natura del segnale digitale e sull'associazione di senso ( vero o falso) o di valore (0 o 1)
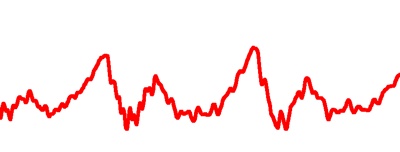
In figura 1 vediamo il segnale sonoro corrispondente alla voce umana. L'ho ottenuto registrando qualche parola con "registratore di suoni" di windows e visualizzando il file con "media player".
Come si vede il segnale è fortemente irregolare ed è "analogo" alla voce, al suono delle parole registrate. Stiamo guardando un segnale analogico.
Diverso il caso rappresentato dalla immagine qui sotto:

Vediamo che i possibili livelli di tensione sono solamente due: "alto" o "basso", non ci sono vie di mezzo, o tutto o niente. Per questo motivo si usa anche associare logicamente ai due livelli alto e basso anche i valori logici "1" o "0", ovvero ancora, in quella che chiameremo logica delle proposizioni, "vero" o "falso".
Adesso quindi abbiamo due immagini da associare ai concetti di analogico e digitale, teniamole di lato perché nel seguito ci serviranno!
Per rispondere alla domanda che da il titolo al capitolo diciamo allora per il momento: l'elettronica digitale è quella che si realizza tramite dispositivi che trattano segnali elettrici la cui natura corrisponde alla Fig. 2. Proseguendo diventerà tutto più chiaro!
Gli oggetti, i componenti dell'elettronica digitale
Presentazione degli integrati, foto di sistemi digitali
Ancora una immagine per cercare di rendere concreto quello di cui stiamo parlando.

L'integrato "7400" (si legge 74 zero-zero), un componente molto semplice, è un classico dei primi esperimenti di elettronica digitale. Il circuito interno ovviamente non è visibile, vediamo il contenitore nero e i piedini di accesso alle varie parti del circuito.
Quest'altro:

è già più complesso, si tratta del famoso "Arduino Uno", dispositivo fondamentale del cosiddetto movimento dei "makers" (per saperne di più consulta: www.repubblica.it/tecnologia/2012/03/08/news/inventori_futuro-31153935/ e http://it.wikipedia.org/wiki/Maker.
Cosa significa "digitale"?
Con il termine digitale indichiamo tutti quei sistemi che, per rappresentare delle grandezze fisiche, adoperano "cifre": lettere e numeri. Un esempio di sistema digitale è quello alfabetico che comprende le lettere dalla A alla Z. Il sistema numerico decimale è anch'esso digitale e costituito dalle cifre da 1 a 9.
In elettronica adoperiamo un particolare sistema digitale detto "binario" in quanto i possibili valori, le possibili cifre, sono solamente due: "0" e "1". Ne abbiamo già parlato poco sopra.
Per contrasto, in che cosa si differenzia dall'analogico?
Spieghiamo più approfonditamente cosa vediamo nella figura 1.
Il segnale, in rosso, va variando in accordo alla voce che l'ha generato. Più tecnicamente, diciamo che stiamo rappresentando una tensione nel suo variare nel tempo cioè una v(t). Sull'asse orizzontale abbiamo il tempo, su quello verticale la tensione (in Volt). La v(t) si dice "continua" (per una definizione matematica vedi: http://it.wikipedia.org/wiki/Funzione_continua qui ci accontenteremo di capire intuitivamente che si tratta di una tensione senza interruzioni) così come continua è la grandezza "suono" presente nell'ambiente nel quale abbiamo fatto la registrazione. Da notare che anche il valore "zero" è un valore della funzione, corrisponde con "silenzio" e non con "niente", che significherebbe che non possiamo dir nulla del valore in quell'intervallo! Semmai il concetto di niente andrebbe associato ad un intervallo di tempo nel quale la funzione "non esiste", la pressione sonora e la tensione non sono descritte in alcun modo (chiarire bene questo conecetto risparmierà molti errori). E ancora notiamo che quando la funzione passa da un valore all'altro percorre nel tempo tutti i valori intermedi: per passare da 1 a 2 per esempio deve necessariamente passare per 1,1 - 1,2 - etc. Lo stesso può dirsi per passare da 1,1 a 1,2. La v(t) assume cioè infiniti valori anche per un intervallo di tempo piccolissimo!
Nella figura 2 vediamo invece che sono presenti solamente due possibili valori: 0 V o 5 V. Non esiste cioè il valore 2 o 3,5! Vediamo inoltre anche graficamente una discontinuità (manca la linea) ad ogni commutazione tra i due valori.
Quindi:
- una grandezza analogica assume sempre infiniti valori per quanto piccolo sia l'intervallo di tempo che stiamo considerando
- una grandezza digitale assume solamente un numero finito e discreto di valori. Nel caso del sistema binario ( quello che ci interessa di più) i valori sono solamente due!
Applicazioni del digitale
Perché l'elettronica digitale è diventata così diffusa?
I motivi dell'affermazione tecnica e commerciale dell'elettronica digitale sono da ricercarsi nella possibilità di semplificare i dispositivi ( che comporta anche una diminuizione dei costi): due livelli di tensione sono più facilmente trattabili di infiniti livelli. Ma anche, forse soprattutto, perché ben si adatta a realizzare dispositivi "logici" e dispositivi di "calcolo". Vediamo di che si tratta.
La logica
Applicare la logica è una cosa che sappiamo fare tutti, in qualche modo è connaturata al processo di crescita dell'individuo. Date certe premesse ne conseguono determinate conclusioni. Espliciteremo tra poco quali siano le "funzioni logiche" che applicheremo in elettronica grazie alle tecnologie digitali.
Il calcolo
Cosa sia il calcolo non c'è certo bisogno di dirlo. Notiamo solamente, ma anche questo è risaputo, che prima dell'invenzione dei computer ( il dispositivo più complesso dell'elettronica digitale) i problemi di calcolo erano molto più onerosi e talmente lunghi da affrontare da costringere gli ingegneri a delle notevoli approssimazioni.
Esempi, esempi!
Qualche esempio di logica.
AND e logica delle proposizioni
La logica delle proposizioni è basata sul concetto di vero o falso. Se dico oggi è lunedì può essere vero o falso (durante gli altri giorni della settimana). Idem se dico oggi piove. Sto quindi considerando due distinte affermazioni ognuna delle quali, separatamente, può essere vera o falsa.
Ma se dico: oggi è lunedì e piove mi riferisco a due condizioni che possono verificarsi simultaneamente. Se non sono un bugiardo ed entrambe le affermazioni sono vere allora anche l'intera proposizione è vera. Basta però che una sola delle affermazioni sia falsa per rendere falsa la proposizione più generale.
Abbiamo appena conosciuto la "funzione logica" AND.
Per descrivere sinteticamente il comportamento della AND si usa la tabella della verità:
| oggi è lunedì | oggi piove | |
| falso | falso | falso |
| falso | vero | falso |
| vero | falso | falso |
| vero | vero | vero |
La stessa tabella vale quando a falso sostituiamo 0 e a vero sostituiamo 1:
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
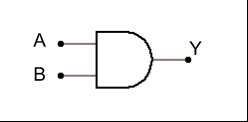
In elettronica digitale esiste un componente chiamato "And" che si indica col seguente simbolo:
L'integrato corrispondente ha la sigla (in logica TTL) 7408:

L'integrato in figura ha ben 14 piedini di collegamento, il simbolo della And invece ne mostra solamente tre! Come mai? La seguente figura svela il "mistero":
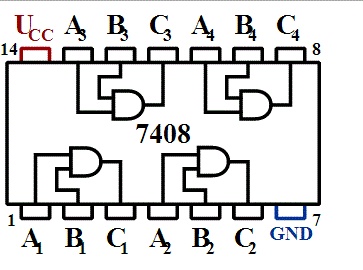
L'integrato contiene 4 "AND". Più i piedini per la tensione di alimentazione Vcc e GND.
Aritmetica binaria
Apparentemente può sembrar strano dover contare on le sole due cifre 0 e 1! Come facciamo? Molto semplice, è spiegato in questo video:
Come si conta con solo 0 e 1
Laboratorio
Montaggio su breadboard di una and e verifica con Led
----------- da fare -----------
Le altre "porte logiche" fondamentali
Conosciamo altri due operatori logici, e quindi in elettronica altre due "porte logiche" che costituiscono il set fondamentale che ci consente di implementare funzione logica volessimo desiderare: si tratta della "OR" e della "NOT"
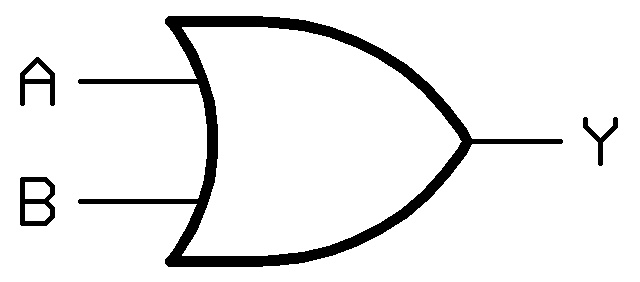
Or
Simbolo e tabella della verità sono i seguenti:
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Corrisponde, in logica proposizionale, alla condizione "o" espressa ad esempio nella frase: il colore della mia prossima giacca dovrà essere nero o grigio. "O" rappresenta la possibilità di una alternativa: infatti vediamo che il risultato è "1" (vero) anche quando solamente una delle variabili di ingresso è uguale ad "1" (vero).
In logica TTL l'integrato corrispondente ha le sigle 7432, 74LS32, etc. La piedinatura è la seguente:
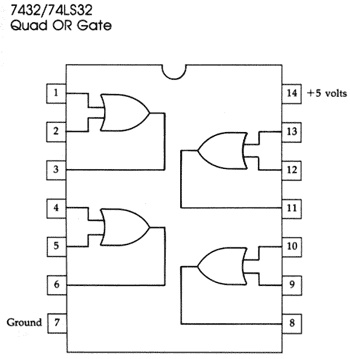
Not
E' l'operatore logico più semplice e coincide con la negazione. Ha un solo ingresso e il simbolo logico è il seguente:
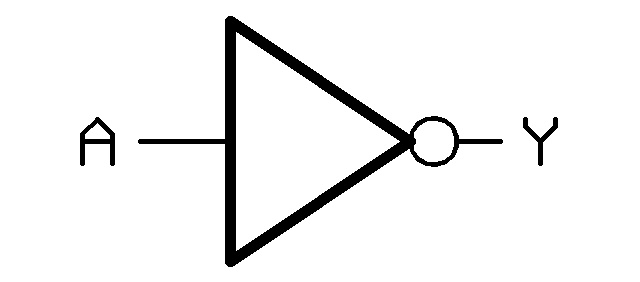
e la tabella della verità:
| A | Y |
| 0 | 1 |
| 1 | 0 |
Avendo due soli connettori nell'integrato corrispondente 7404 - 74LS04 troveremo 6 porte not con la seguente piedinatura:
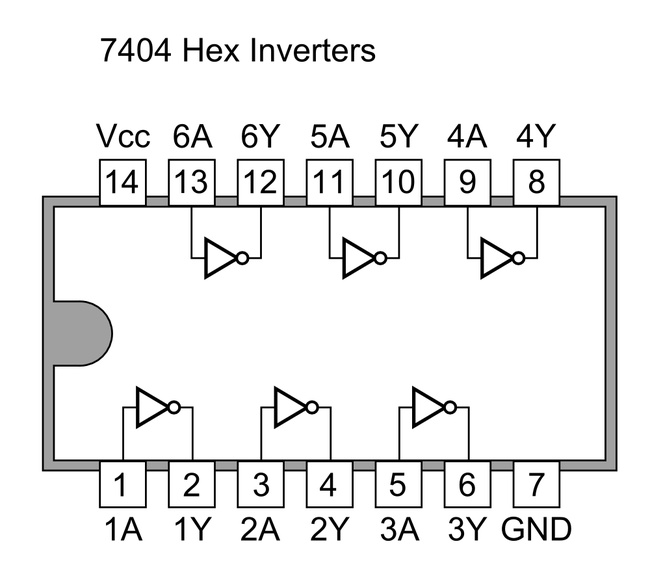
Analisi dei Circuiti Logici
Le tre porte logiche che abbiamo conosciuto consentono, opportunamente combinate, la realizzazione di qualsiasi funzione logica. Vediamo subito un esempio:
Interpretare il circuito
Come abbiamo visto nel video il circuito è disegnato in modo tale da consentire una lettura dello stesso da sinistra verso destra: gli ingressi sono a sinistra, le uscita e destra di ogni componente. Ovviamente questa non è una regola assoluta sempre rispettata, quindi bisogna sempre stare attenti a distinguere gli ingressi dalle uscite. Si tratta in pratica di applicare pur sempre il principio di causa ed effetto....Una volta che questo sia chiaro, diventa facile seguire la propagazione dei valori logici dall'uscita di una porta all'ingresso della successiva. In caso di dubbio quanto riportato nel video dovrebbe essere in grado di aiutare.
Ricavare la funzione logica
Nel video abbiamo già ricavato una èrima volta la funzione logica di un circuito combinatorio. Facciamolo un'altra volta per un circuito appena più complesso, questa volta fermandoci sui singoli passi.
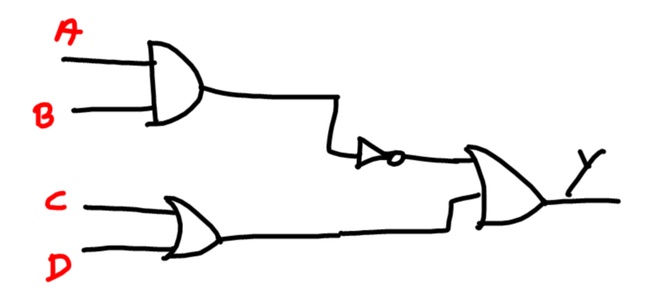
Una possibilità di lavoro è data dal "partire dalla fine". L'uscita Y a quale porta logica corrisponde? Dalla figura vediamo che si tratta di una "OR", quindi possiamo comnciare a scrivere:

nella quale il segno "+" sta per "somma logica" ( attenzione! diversa da quella aritmetica . . .), quindi "OR".
Il passo successivo consiste nel vedere cosa scrivere al posto dei puntini.
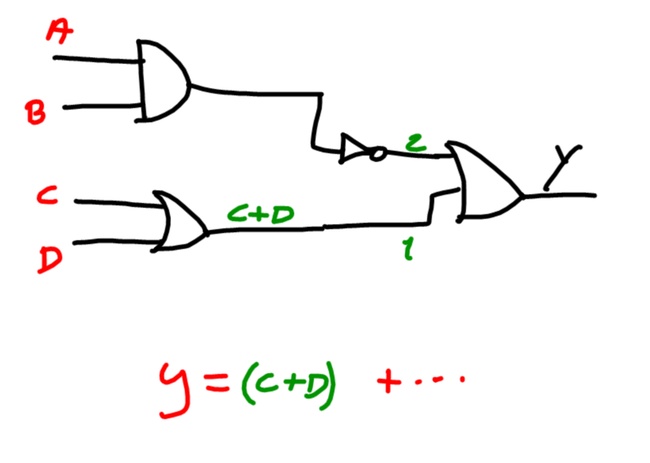
Se indichiamo con "1" l'ingresso indicato in verde, notiamo subito che si tratta dell'uscita della or che ha in ingresso le variabili logiche "C" e "D", quindi in 1 avremo (C+D).
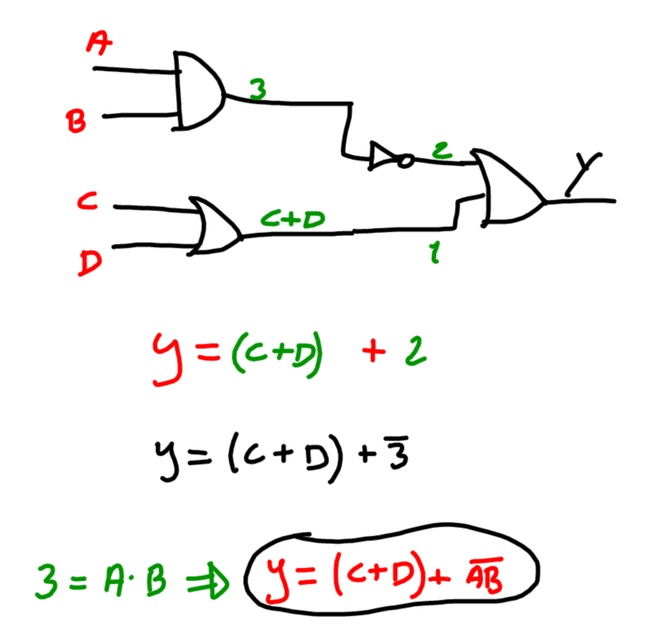
Se con "2" indichiamo l'altro ingresso della OR terminale ci accorgiamo subito che si tratta del negato di "3", cioè del negato della and tra A e B.
Il risultato finale è quello indicato nella formula in rosso cerchiata. Non difficile!
Costruire la tabella di verità
Abbiamo visto le tabelle di verità delle singole porte logiche fondamentali. Vedremo adesso come ricavare le tabelle di verità di una funzione logica qualsiasi, ad esempio quella che abbiamo appena ricavato:
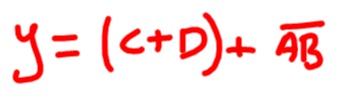
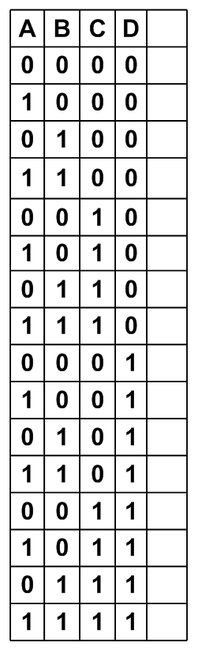
La prima domanda alla quale dobbiamo rispondere è: quante righe avrà questa tabella? La risposta è semplice, dobbiamo calcolare quanto fa 2 elevato al numero di variabili logiche, nel caso specifico
Dunque faremo una tabella con 16 righe! Le prime quattro colonne avranno come intestazione il nome delle variabili logiche:

Adesso vediamo come scrivere tutte le differenti combinazioni dei valori delle variabili di ingresso senza dimenticarne nemmeno una.
Procederemo così:
- nella prima colonna scriveremo una successione di "0" e "1" cambiando valore ad ogni riga
- nella seconda colonna la successione vedrà due "0" seguiti da due "1" e così via
- nella terza colonna la successione vedrà quattro "0" seguiti da quattro "1" e così via
- nella quarta colonna la successione vedrà otto "0" seguiti da otto "1" e così via
Così compilata la tabella si presenterà in questo modo:
Ora aggiungiamo alla tabella le colonne che ci serviranno a ricavare prima le due funzioni logiche parziali la "2" e la "1" e infine la "y", l'uscita.
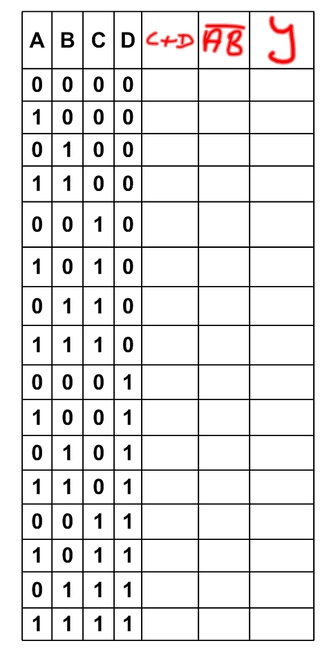
e procediamo alla compilazione come indicato nel seguente video:
La tabella compilata avrà infine questo aspetto:
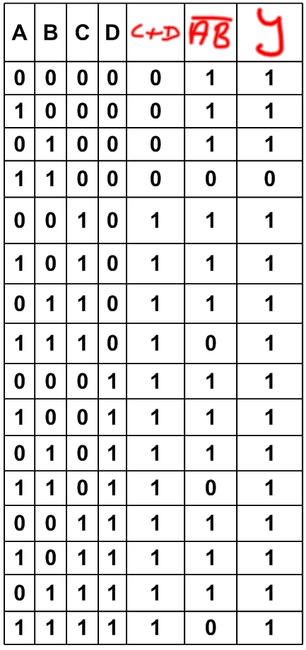
Possiamo quindi dire di avere imparato:
- ad analizzare un semplice circuito logico combinatorio
- a ricavare la funzione logica di uscita
- a compilarne la tabella di verità.
Porte logiche universali
In aggiunta alle porte And, Or e Not che abbiamo conosciuto esistono delle altre porte logiche il cui utilizzo è molto prezioso: vediamole.
Nand
Si tratta di una And negata. L'uscita sarà quindi sempre a livello alto tranne nel caso in cui entrambi gli ingressi sono a livello alto. La tabella di verità è quindi la seguente:
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
con
Il simbolo logico è il seguente:
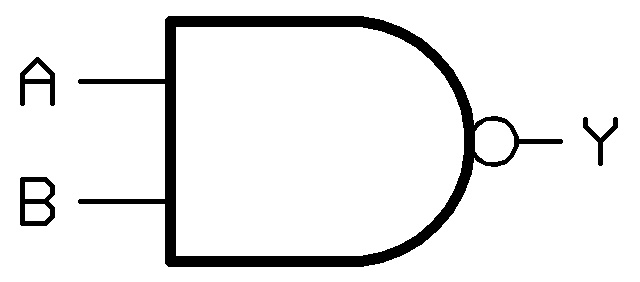
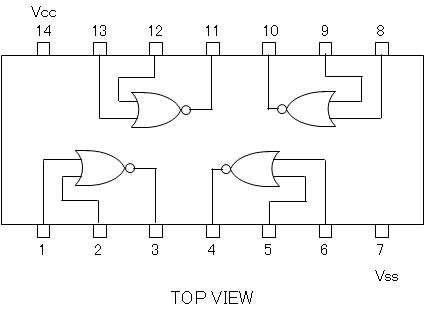
e questa la piedinatura dell'integrato 7400 (74LS00):
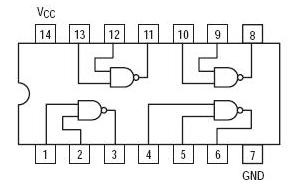
Nor
Si tratta di una Or negata. L'uscita sarà quindi sempre a livello basso tranne nel caso in cui entrambi gli ingressi sono a livello basso. La tabella di verità è quindi la seguente:
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Il simbolo logico è il seguente:
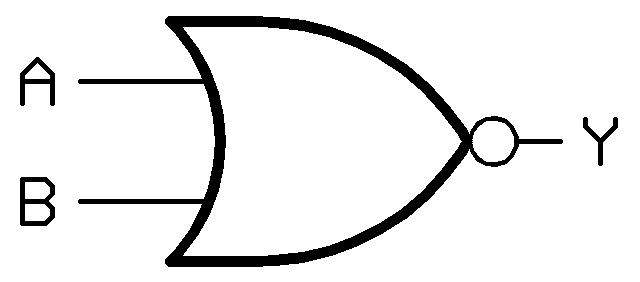
e questa è la piedinatura dell'integrato 7402
Adesso che le abbiamo conosciute proviamo a rispondere a questa domanda: perché Nor e Nand vengono dette "universali"? Semplice! Perchè da sole possono essere utilizzate per ottenere le funzioni logiche fondamentali e quindi tutte le possibili funzioni logiche.
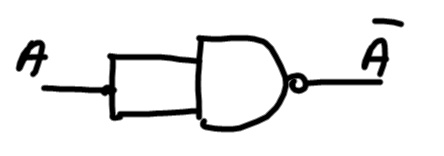
Ad esempio da una Nand è facilissimo ottenere una Not, basta inviare la stessa variabile logica ai due ingressi:
E quindi una And realizzata con sole "nand" sarà:

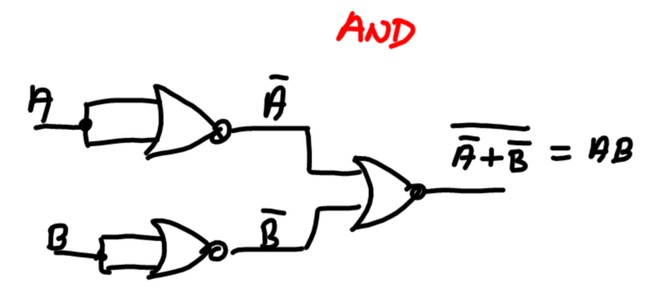
Un po' più complesso il caso della realizzazione di una or con sole nand:
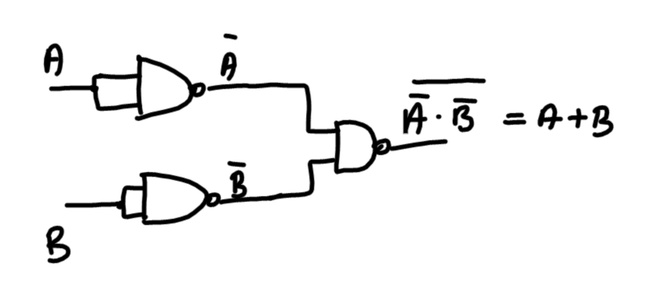
In questo caso per la dimostrazione dobbiamo scomodare il teorema di de Morgan (vedi qualsiasi testo o in rete), oppure fare la prova confrontando riga per riga le due tabelle di verità.
Analogamente, con sole "NOR", avremo:

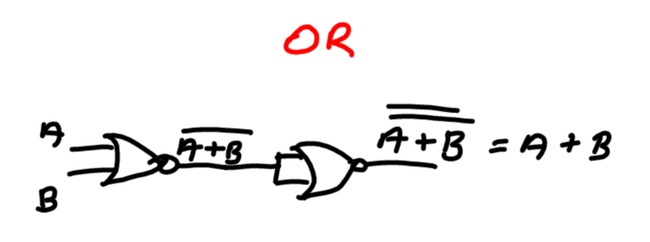
Progetto dei circuiti logici
Che significa "progetto" di un circuito logico? Si tratta di fare esattamente il contrario di quanto visto sinora. Sin qui abbiamo imparato a ricavare funzione logica e tabella di verità di un dato circuito logico.
Ora invece impareremo a creare un circuito logico a partire da una tabella di verità.
Mi sembra che la trattazione sul libro di testo sia piuttosto facile da seguire, quindi vi rimando senz'altro alla lettura delle pagine 124---> 127
Mappe di Karnaugh
Qui di seguito un breve videotutoriale per spiegare molto semplicemente come si utilizza una mappa di Karnaugh (nel video ho adoperato la pronuncia che sentirete un pò dappertutto, ma non sono affatto sicuro che si trattai di quella corretta, me ne scuso):
Porte logiche speciali
Esistono ancora delle porte logiche che non rientrano nelle precedenti categorie: si tratta dell'OR esclusivo e del NOR esclusivo
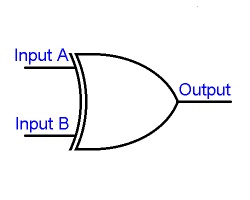
Ex-Or
Ovvero OR Esclusivo. L'uscita è a livello alto quando gli ingressi sono diversi. La tabella di verità è la seguente:
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Il simbolo logico è il seguente:
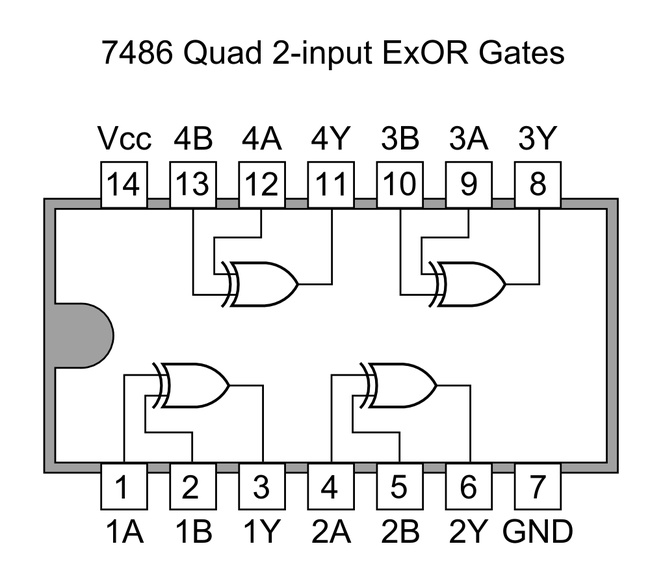
e questa è la piedinatura dell'integrato:
Ex-Nor
Ovvero NOR Esclusivo. L'uscita è a livello alto quando gli ingressi sono uguali. La tabella di verità è la seguente:
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Questo il simbolo logico
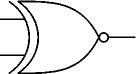
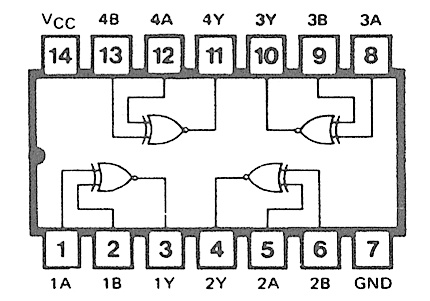
e questa la piedinatura:
Un circuito che fa semplici somme
Il motivo per il quale sono importanti le porte logiche appena trattate risiede nella possibilità, tra l'altro, di costruire circuiti che fanno la somma aritmetica di numeri binari. Qui nel seguito vediamo il funzionamento del full adder ( in italiano "sommatore pieno"), un dispositivo per sommare due numeri a un bit. E' la base per qualsiasi altro sommatore che operi su numeri a più bit.
Full-adder
Si rimanda al testo in adozione (pag. 130) per lo schema elettrico e le ulteriori spiegazioni. Nel video che segue troverete la spiegazione su come si sommano due bit e come funziona il circuito che fa la somma.
Questo il link per eseguire la simulazione on line mostrata nel video: http://www.falstad.com/circuit/e-fulladd.html