Types of Angles

Vertically opposite angle

Vertical angles are two non-adjacent angles formed by intersecting lines. 1 and 3 are vertical angles and 2 and 4 are vertical angles.

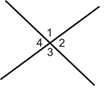
The Vertical Angles Theorem states that if two angles are vertical angles, then they are congruent.

Pair of Lines

Transversal: A line that intersects two distinct lines. These two lines may or may not be parallel

Many math problems involve the intersection of three or more lines. Examine the diagram below

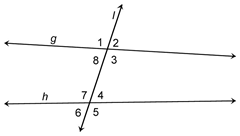
In the diagram, lines g and h are crossed by line l. We have quite a bit of vocabulary to describe this situation:

·         Line l is a transversal because it intersects two other lines (g and h). The intersection of line l with g and h forms eight angles as shown.

·         The area between lines g and h is called the interior of the two lines. The area not between lines g and h is called the exterior.

·         Angles 1 and 2 are called adjacent angles because they share a side and do not overlap. There are many pairs of adjacent angles in this diagram, including 2 and 3, 7 and 4, and 8 and 1.

·         1 and 3 are vertical angles. They are nonadjacent angles made by the intersection of two lines. Other pairs of vertical angles in this diagram are 2 and 8, 4 and 6, and 5 and 7.

·         Corresponding angles are in the same position relative to both lines crossed by the transversal. 1 is on the upper left corner of the intersection of lines g and l. 7 is on the upper left corner of the intersection of lines h and l. So we say that 1 and 7 are corresponding angles.

·         3 and 7 are called alternate interior angles. They are in the interior region of the lines g and h and are on opposite sides of the transversal.

·         Similarly, 2 and 6 are alternate exterior angles because they are on opposite sides of the transversal, and in the exterior of the region between g and h.

·         Finally, 3 and 4 are consecutive interior angles. They are on the interior of the region between lines g and h and are next to each other. 8 and 7 are also consecutive interior angles.

Checking for Parallel Lines

Parallel lines are two or more lines that lie in the same plane and never intersect.

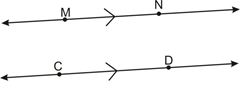
When we draw a pair of parallel lines, we use an arrow mark > to show that the lines are parallel. Just like with congruent segments, if there are two (or more) pairs of parallel lines, we use one arrow > for one pair and two (or more) arrows >> for the other pair.

Example :

1.      Which of the following best describes parallel lines?

a.       They lie in the same plane but do not intersect.

b.      They intersect, but not at a right angle.

c.       They lie in different planes and never intersect.

d.      They intersect at a right angle

Ans=a

(source- mrudula, 4-6-13 , Parallel Lines)

We say two lines are parallel to each other if

1.      Their slops are equal

2.      If the have a common normal.

3.      When a transversal cuts the two lines then their

·         Corresponding angles are equal

·         Pair of Interior Alternate angles are equal

(source- mrudula, 4-6-13 , Parallel Lines)