ความเป็นมาของแคลคูลัส (A brief history of calculus)

บทนำ

แคลคูลัส เป็นคณิตศาสตร์แขนงหนึ่งที่มีพี้นฐานมาจากการศึกษาการเปลี่ยนแปลงและการเคลื่อนที่ทางกลศาสตร์ การสร้างรากฐานวิชาให้รัดกุมจำเป็นต้องอาศัยความรู้ทางคณิตศาสตร์ที่ซับซ้อน การพัฒนาความรู้จึงต้องละบริบททางวิทยาศาสตร์ที่ไม่จำเป็นออกไป เพื่อให้ได้ระบบภาษาสัญลักษณ์ที่มีความกระชับ ชัดเจน และสามารถขยายความรู้ต่อยอดออกไปเรื่อย ๆ ด้วยเหตุผลนี้ส่วนหนึ่งทำให้แคลคูลัสพัฒนาแยกตัวออกมาจากวิทยาศาสตร์และเข้าใกล้คณิตศาสตร์บริสุทธิ์มากขึ้น การพัฒนาแคลคูลัสในแง่มุมว่าเป็นคณิตศาสตร์แขนงหนึ่ง เริ่มเห็นชัดในคริสต์ศตวรรษที่ 17 จากผลงานของนิวตัน (Isaac Newton, 1643 – 1727, England) และไลบ์นิต (Gottfried Wilhelm van Leibniz, 1646 – 1716, Germany) แคลคูลัสเริ่มพัฒนาตัวเองไปสู่คณิตศาสตร์วิเคราะห์ที่ให้ระบบการให้เหตุผลที่มีความรัดกุมมากกว่าเดิม เมื่อ โคชี (Augustin Louis Cauchy, 1789 – 1857, France) ได้เสนอให้ใช้แนวคิดของลิมิตของฟังก์ชันเพื่อเป็นรากฐานความรู้ของแคลคูลัส เกิดการแสวงหาความรู้ต่อยอดต่าง ๆ ทางคณิตศาสตร์ และสะท้อนกลับนำไปใช้ประโยชน์ในการแสวงหาความรู้ทางวิทยาศาสตร์และวิศวกรรมศาสตร์ และแน่นอนว่ามนุษย์ยังแสวงหาวิทยการเพื่อสร้างเทคโนโลยีตอบสนองความต้องการของตัวเองตลอดเวลา นั่นหมายถึงจะมีหลายปัญหาที่ยังไม่แก้ไม่ได้ด้วยความรู้ที่มีในปัจจุบัน การแสวงหาความรู้ใหม่ ๆ จะย้อนกลับไปผลักดันให้แต่ละวิชาไม่หยุดที่จะพัฒนาความรู้ของตัวเอง แคลคูลัสก็เป็นหนึ่งแขนงวิชา ดังนั้นการทราบที่มาของการพัฒนาและความรู้พื้นฐานสุดของแคลคูลัส จะทำให้เห็นแนวทางในการพัฒนาความรู้ต่อไป

ยุคโบราณ

มนุษย์รู้จักค้นคว้าความรู้และบันทึกไว้เพื่อการถ่ายทอดส่งต่อความรู้ตั้งแต่ยุคหิน แต่ความรู้ที่ถือได้ว่าอยู่ในขอบข่ายและเป็นรากฐานเริ่มต้นของแคลคูลัส คือ ความรู้เกี่ยวกับการแก้ปัญหาการวัด หลักฐานที่ค้นพบมีอายุก่อนคริสต์ศักราช เช่น บันทึกบนกระดาษปาปีรัส (Papyrus) ของชาวอียิปต์โบราณ บันทึกบนแผ่นดินเหนียวของชาวบาบิโลน แต่ก็ยังไม่ทราบแน่ชัดว่าคนสมัยนั้นได้ความรู้เหล่านี้มาได้อย่างไร ไม่พบหลักฐานว่ามีการให้เหตุผลทางตรรกวิทยาเพื่อรองรับความรู้ที่ได้มาดังกล่าว การแก้ปัญหาบางอย่างไม่อาจระบุได้ว่าผลที่ได้เป็นค่าประมาณหรือค่าจริง อย่างเช่น ในบันทึกของอาเมส (Ahmose, ~1680 - 1620BC, Egypt) ชี้ว่า ชาวอียิปต์โบราณมีความรู้ว่าปริมาตรของพีระมิดฐานสี่เหลี่ยมจัตุรัสเป็น 1/3 เท่าของปริมาตรของปริซึมที่มีฐานเดียวกันและสูงเท่ากัน (ซึ่งในปัจจุบันพบว่าความรู้นี้ถูกต้อง แต่การได้มาซึ่งความรู้นี้ ต้องอาศัยระบบคณิตศาสตร์ที่พัฒนาหลายพันปีต่อมาเพื่อแสดงเหตุผลที่มาของผลลัพธ์)

สมัยกรีกโบราณ เป็นยุครุ่งเรืองของการใช้ตรรกวิทยาในการแสวงหาความรู้ มีบันทึกถึงความรู้ของนักปรัชญาชาวกรีกหลายชิ้น แต่ที่อาจนับได้ว่าเป็นจุดเริ่มต้นของแคลคูลัสในยุคนี้ ได้แก่ The Method of Exhaustion (แม่แบบความรู้เกี่ยวกับปริพันธ์ในแคลคูลัสที่เราทราบในปัจจุบัน) ผู้ที่ถือว่าได้เสนอแนวคิดเกี่ยวกับระเบียบวิธีนี้ คนแรก ๆ คือ 

แอนติฟอน (Antiphon the Sophist, ~480 - 411BC, Greece) โดยใจความสำคัญที่ระเบียบวนี้ให้ไว้คือ จะมีกระบวนการที่ทำให้เราเข้าถึงค่าจริงของคำตอบโดยเริ่มจากค่าประมาณค่าหนึ่งได้อย่างไม่จำกัด เช่น ในการหาพื้นที่ของรูปวงกลม ระเบียบวิธีนี้ให้กระบวนการเข้าถึงค่าจริงของพื้นที่ของรูปวงกลมนี้ไว้ประมาณว่า เริ่มจากสร้างรูปหลายเหลี่ยมแนบในวงกลม โดยสังเกตได้ว่า หากจำนวนเหลี่ยมมากขึ้น ผลต่างของพื้นที่ของรูปทั้งสองจะหมดไป แต่ก็มีข้อแย้งในเชิงปฏิบัติว่าเราจะสามารถสร้างรูปหลายเหลี่ยมให้มีจำนวนเหลี่ยมได้มากมายแค่ไหนกัน (อุปมาในปัจจุบันก็ประมาณว่า เรายังไม่สามารถหาค่าจริงของจำนวนอตรรกยะ π ได้ด้วยคอมพิวเตอร์ที่มีอยู่)

คนกรีกโบราณเป็นผู้ที่ยึดมั่นกับความรู้และการให้เหตุผลทางตรรกะที่ต้องรัดกุมเข้มงวด  ข้อแย้งหนึ่งที่เกิดขึ้ดต่อ The Method of Exhaustion เช่น รูปหลายเหลี่ยมก็คือรูปหลายเหลี่ยม รูปวงกลมก็คือรูปวงกลม กระบวนการที่จะทำให้รูปหลายเหลี่ยนปรับเปลี่ยนไปเป็นรูปวงกลม มันสมเหตุสมผลหรือไม่ หรือกล่าวอีกนัยหนึ่งว่า มีผู้ที่ปฏิเสธการแบ่งขนาด ไม่ว่าจะเป็น ความยาว พื้นที่ ปริมาตร หรือเวลา อย่างไม่จำกัด ตัวอย่างของข้อปฏิเสธนี้ เช่น จากผลงานของ ซีโนแห่งอีเลีย (Zeno of Elea, ~490 – 430BC, Italy) ผู้ที่ได้เสนอข้อความที่ขัดแย้งกับสามัญสำนึกทั่วไป หรือคำศัพท์ภาษาไทยเราเรียกว่า ปฏิทรรศ์ ซึ่งปฏิทรรศ์ของซีโน (Zeno’s paradoxes) ข้อหนึ่งที่จี้จุดบกพร่องทางตรรกะ หากเราสามารถแบ่งขนาดได้อย่างไม่จำกัด มีใจความในทำนองที่ว่า 

“หากพิจารณาการเคลื่อนที่ของวัตถุจากจุด A ไปจุด B ก่อนที่จะถึงจุด B วัตถุนั้นจะต้องเคลื่อนที่ผ่านจุดกึ่งกลางระหว่างจุดทั้งสอง เรียกจุดกึ่งกลางนั้นว่า M1 ในทำนองเดียวกัน ก่อนที่จะถึงจุด M1 วัตถุจะต้องเคลื่อนที่ผ่านจุดซึ่งเป็นจุดกึ่งกลางระหว่างจุด A และจุด M1 เรียกจุดกึ่งกลางที่สองนี้ว่า M2 พิจารณาเช่นนี้เรื่อยไป จะเห็นว่าวัตถุจะต้องเดินทางผ่านจุด M3, M4, M5, ... เป็นจำนวนมากมายเป็นอนันต์ หรือสามารถกล่าวอีกนัยหนึ่งว่าเป็นไปไม่ได้เลยที่มีการเคลื่อน จึงเกิดข้อขัดแย้งทางสามัญสำนึกหรือข้อปฏิทรรศ์”

ปฏิทรรศ์ของซีโนได้นำไปสู่แนวคิดของสิ่งที่เรียกว่า ขนาดที่แบ่งย่อยไม่ได้อีก (infinitesimals) ซึ่งต่อมา ลูซิปปัส (Leucippus, ~480 - 420BC, Turkey) และเดโมคริตัส (Democritus, ~460 - 370BC, Greece) ได้ขยายแนวคิดนี้เพื่อเสนอแนวคิดที่ว่า 

ขนาดจะประกอบไปด้วย อนุภาคมูลฐานที่แบ่งย่อยไม่ได้ (indivisible elements หรือ atom) จำนวนจำกัดจำนวนหนึ่ง 

อาริสโตเติล (Aristotle, ~384 – 322BC, Greece) ได้ใช้หลักการเดียวกันนี้ไปเขียนถึง เส้นที่แบ่งย่อยไม่ได้อีก (indivisible line) แต่แนวคิดของ ขนาดที่แบ่งไม่ได้ นี้ก็ไม่มีความรัดกุมพอที่จะนำไปใช้ในการให้เหตุผลทางคณิตศาสตร์ เพื่อหลีกเลี่ยงข้อขัดแย้งทางตรรกะและการใช้แนวคิดของขนาดที่แบ่งย่อยไม่ได้อีกโดยตรง ยูโดซุส (Eudoxus of Cnidus, ~390 - 340BC, Turkey]) จึงได้ปรับปรุงการให้เหตุผลเกี่ยวกับ The Method of Exhaustion ให้มีความรัดกุมมากขึ้น โดยอาศัยความรู้ทางเรขาคณิตช่วยในพิจารณาขนาดที่แบ่งไม่ได้อีกในทางอ้อม โดยพิจารณาผ่านอัตราส่วนของขนาดที่วัดได้ทางเรขาคณิต ซึ่งต่อมาภายหลังความรู้เหล่านี้ได้ปรากฎในผลงานของ ยุคลิด (Euclid of Alexandria, ~365 – 275BC, Egypt) 

ส่วนผู้ที่ใช้ความรู้จากระเบียบวิธีนี้จนได้ผลงานที่ถือได้ว่ามีแนวคิดใกล้เคียงกับแนวคิดของการหาปริพันธ์ในแคลคูลัสที่ทราบกันแล้วในปัจจุบันคือ อาร์คิมีดีส (Archimedes, ~287 – 212BC, Italy) ตัวอย่างผลงานที่เด่นซึ่งทำให้แนวคิดของกระบวนการเข้าถึงค่าจริงอย่างไม่จำกัดชัดเจนยิ่งขึ้น ได้แก่ วิธีการหาพื้นที่ที่ปิดล้อมด้วยพาราโบลาตัดกับเส้นตรง หรือเรียกว่า เซกเมนต์ของพาราโบลา (The quadrature of parabola) เพื่อให้เห็นแนวคิดจากระเบียบวิธีที่อาร์คิมีดีสได้ปรุงปรับ ขอยกตัวอย่างที่เรียบเรียงจากวิกิพีเดีย ดังนี้

กระบวนการในระเบียบวิธีนี้เริ่มต้นโดยสร้างรูปสามเหลี่ยมรูปหนึ่งให้แนบในเซกเมนต์ของพาราโบลา นั่นคือต้องให้ด้านหนึ่งของรูปสามเหลี่ยมอยู่บนส่วนของเส้นตรงที่ปิดล้อม อีกสองด้านที่เหลือของรูปสามเหลี่ยมจะแบ่งพื้นที่ของเซกเมนต์เริ่มต้นออกเป็นเซกเมนต์ย่อยสองเซกเมนต์ ซึ่งพื้นที่ของเซกเมนต์ย่อยทั้งสองเมื่อรวมกับพื้นที่ของรูปสามเหลี่ยมจะเท่าพื้นที่ของเซกเมนต์เริ่มต้น ทำการสร้างรูปสามเหลี่ยมแนบในเซกเมนต์ย่อยทั้งสองโดยมีเงื่อนไขเดียวกับการสร้างรูปสามเหลี่ยมรูปแนบในรูปแรก นั่นคือให้ด้านหนึ่งของรูปสามเหลี่ยมอยู่บนส่วนของเส้นตรงที่ปิดล้อมเป็นเซกเมนต์ ดำเนินกระบวนการนี้ไปเรื่อย ๆ แล้วจะได้ว่าพื้นที่ของเซกเมนต์ของพาราโบลาหาได้จากผลบวกของพื้นที่ของแต่ละรูปสามเหลี่ยม แล้วถ้าสามารถดำเนินกระบวนการนี้ได้อย่างไม่จำกัด จะได้ค่าที่แท้จริงของพื้นที่ของเซกเมนต์ของพาราโบลา (ดูรูปด้านล่างประกอบ)

จากกระบวนการสร้างข้างต้น ทำให้ทราบว่าพื้นที่ของเซกเมนต์ของพาราโบลาจะเป็น 4/3 เท่าของพื้นที่ของรูปสามเหลี่ยมรูปแรกที่สร้างให้แนบในเซกเมนต์ของพาราโบลานั้น (ซึ่งต่อมาทราบว่าเป็นผลบวกของอนุกรมเรขาคณิตอนันต์ ที่มีอัตราส่วนร่วมเป็น 1/4) อาร์คิมีดีส ยังได้พัฒนาต่อยอดระเบียบวิธีเพื่อใช้หาพื้นที่ผิวและปริมาตรของทรงเรขาคณิตแบบต่าง ๆ จนได้ระเบียบวิธีที่ต่อมาเรียกว่า The method of Archimedes หรือ Method of equilibrium โดยมีแนวคิดของแบ่งย่อยทรงเหล่านั้นออกเป็นแผ่นบาง ๆ ตามแนวศูนย์ถ่วง แล้วหาผลบวกของขนาดของแผ่นบาง ๆ เหล่านั้น ถึงแม้จะไม่มีคณิตศาสตร์ที่รัดกุมรองรับ แต่ถือว่าเป็นภาพแสดงแนวคิดคราว ๆ ของการหาปริพันธ์ในแคลคูลัสที่ทราบในปัจจุบัน

ยุคกลาง

ในยุคกลาง การพัฒนาแคลคูลัสไม่มีการก้าวกระโดดมากนัก แนวคิดและวิธีการส่วนใหญ่ยังอิงอยู่กับการวัด การเขียนกราฟ และการแบ่งระนาบออกเป็นหน่วยเล็กๆ ที่ไม่สามารถแบ่งได้อีก ต่อเนื่องมาจนถึงคริสต์ศตวรรษที่ 16 เมื่อวิศวกรรมศาสตร์เครื่องกลมีความต้องการที่จะใช้คณิตศาสตร์ที่รัดกุมในการแก้ปัญหาเกี่ยวกับจุดศูนย์ถ่วง ผลงานที่เกี่ยวข้องกับการพัฒนาแนวคิดของแคลคูลัสลำดับได้ดังนี้

วาเลริโอ (Luca Valerio, 1553-1618, Italy) ได้ตีพิมพ์ผลงานที่ได้รับแรงบันดาลใจมาจาก The method of Archimedes ภาพแสดงแนวคิดของปริพันธ์ในแคลคูลัสเริ่มชัดขึ้น

เคปเลอร์ (Johannes Kepler, 1571 - 1630, Germany)ได้พัฒนาวิธีการหาพื้นที่ของเซกเตอร์ของวงรีโดยพิจารณาว่าพื้นที่เป็นผลรวมของเส้น

คาวาลีเอรี (Bonaventura Francesco Cavalieri, 1598 - 1647, Italy) ได้ขยายแนวคิดให้ชัดเป็นระเบียบวิธีที่เรียกว่า Method of indivisible โดยมองว่า 

เส้นตรงประกอบด้วยจุดเป็นจำนวนอนันต์ พื้นที่ผิวประกอบด้วยเส้นจำนวนอนันต์ และปริมาตรประกอบด้วยพื้นที่ผิวจำนวนอนันต์ 

ทำให้ได้เทคนิคการหาพื้นที่ของรูปสามเหลี่ยมมุมฉาก โดยการแบ่งย่อยพื้นที่ออกเป็นส่วนประกอบเล็กๆ เกือบเป็นเส้น แล้วหาผลรวมของเส้นเหล่านี้ ซึ่งแนวคิดนี้คล้ายกับที่ชาวกรีกโบราณได้เสนอไว้ แต่วิธีคิดแบบใหม่นี้มีการให้เหตุผลทางคณิตศาสตร์ที่รัดกุมกว่ารับรอง ซึ่งจากการพิจารณาปัญหาข้างต้น สามารถแปลงไปเป็นปัญหาของการหาค่าของนิพจน์ 

 ซึ่งเมื่อให้จำนวนเต็มบวก n มีค่ามากขึ้น นิพจน์ดังกล่าวจะมีค่าเข้าใกล้ 1/2  และปัญหาในทำนองเดียวกันในสามมิติ ระเบียบวิธีดังกล่าวให้เทคนิคการหาปริมาตรของกรวย และสามารถแปลงปัญหามาเป็นการพิจาณาหาค่าของนิพจน์

ซึ่งเมื่อให้จำนวนเต็มบวก n มีค่ามากขึ้น นิพจน์ดังกล่าวจะมีค่าเข้าใกล้ 1/3  หมายเหตุ ลองใช้ Answer Engine หาลิมิตลำดับนี้ดู lim of (1^2+2^2+3^2+...+n^2)/(n^2(n+1))

โรแบร์วาล์ (Gilles Personne de Roberval, 1602 - 1675, France) ได้พิจารณาปัญหาทำนองเดียวกับ คาวาลีเอรี จนได้ปัญหาของการหาค่าของนิพจน์ 

และพบว่านิพจน์นี้มีค่าเข้าใกล้ 

เมื่อให้จำนวนเต็มบวก n มีค่ามากขึ้น สำหรับจำนวนเต็มบวก m ใด ๆ

แฟร์มา (Pierre de Fermat, 1601 - 1665, France) ได้ข้อสรุปเช่นเดียวกับ โรแบร์วาล์ และนอกจากนี้ยังสามารถขยายบทพิสูจน์เพื่อแสดงว่า m สามารถเป็นได้ทั้งจำนวนเต็มลบหรือเศษส่วน จะเห็นว่าการพิจารณาให้จำนวนเต็มบวก n มีค่ามากขึ้นได้และทำได้อย่างไม่จำกัด เป็นตัวอย่างการอ้างอิงความรู้ทางคณิตศาสตร์ที่รัดกุมและเข้มงวดกว่า ในการยืนยันแนวคิดของกระบวนการ การเข้าถึงค่าแท้จริงของผลเฉลยอย่างไม่จำกัด (ซึ่งชาวกรีกโบราณได้เสนอแนวคิดไว้แล้วนั้น) ผลงานของแฟร์มาที่ถือว่ามีบทบาทสำคัญต่อการพัฒนาแนวคิดของแคลคูลัสแบบก้าวกระโดด ซึ่ง ลากรองช์ (Joseph Louis Lagrange, 1736 - 1813, France) ถึงกับยกย่องให้แฟร์มาว่าเป็นผู้คิดค้นแคลคูลัสแนวใหม่  ได้แก่ 

การแก้ปัญหาค่าสูงสุดหรือต่ำสุดโดยอาศัยความรู้ทางเรขาคณิต (ในปัจจุบันทราบกันว่าเป็น แคลคูลัสเชิงอนุพันธ์) ซึ่งให้หลักการแปลงปัญหาไปเป็นการแก้ปัญหาเกี่ยวกับ การหาจุดบนเส้นโค้งที่ทำให้เส้นสัมผัสเส้นโค้ง ณ จุดนั้นขนานกับแกนนอน

ความรู้เกี่ยวกับ เส้นสัมผัสเส้นโค้ง (tangent line) ปรากฏนานแล้ว ดังจะเห็นได้จากผลงานของ แปปปัส (Pappus of Alexandria, ~290 - 350AD, Greece) และในยุคกลางนี้ จากผลงานของ โอเรสเม (Nicolas Oresme, ~1323 - 1382, France) ทำให้ทราบว่า ค่าต่ำสุดหรือสูงสุงของเส้นโค้งจะอยู่บริเวณที่มีการเปลี่ยนแปลงค่าของตัวแปรช้าที่สุด จากจุดนี้ถือได้การพัฒนาแคลคูลัสเริ่มอยู่บนรากฐานแขนงของคณิตศาสตร์ที่เรียกว่า เรขาคณิตวิเคราะห์ โดยความรู้ทางคณิตศาสตร์ของความชันของเส้นสัมผัสเส้นโค้ง สามารถนำมาอธิบายได้อย่างรัดกุมถึงแนวคิดของ อัตราส่วนของสองขนาดที่ไม่สามารถแบ่งแยกได้อีก ซึ่งปรากฏอยู่ในระเบียบวิธีที่แรกเริ่มที่เสนอโดยชาวกรีกโบราณ

จากหลักฐานการติดต่อแลกเปลี่ยนความรู้กับ เดการ์ต (René Descartes, 1596 - 1650, France) ทำให้ทราบว่า แฟร์มา ได้เสนอ 

หลักการของการแก้ปัญหาค่าต่ำสุดหรือค่าสูงสุดว่าเป็นการแก้สมการเพื่อหาจุดที่ทำให้ความชันของเส้นสัมผัสเส้นโค้งเป็นศูนย์ (อย่างที่ทราบแล้วในปัจจุบัน)

เริ่มมีผลงานที่เกี่ยวกับการพัฒนาแคลคูลัสต่อจากแฟร์มามากขึ้น ซึ่งผลงานหลายชิ้นได้มีส่วนในการพัฒนาแคลูลัสแบบคู่ขนานของนิวตันและไลบ์นิตซ์ (ทั้งสองที่ได้ชื่อร่วมกันว่าเป็นผู้ประดิษฐ์ แคลคูลัส ถึงแม้จะพัฒนาความรู้ทางแคลคูลัสอย่างอิสระต่อกัน แต่มีหลักฐานเชื่อมโยงบุคคลทั้งสองในทางอ้อม ซึ่งเป็นจดหมายโต้ตอบความรู้ระหว่างเพื่อนร่วมงานของบุคคลทั้งสอง โดยพบว่าเพื่อนร่วมงานของทั้งสองหลายคนเป็นนักคณิตศาสตร์คนเดียวกัน บุคคลเหล่านั้น เช่น

บัวเนอร์ (Florimond de Beaune, 1601-1652, France)  ผู้ขยายระเบียบวิธีทางเรขาคณิตวิเคราะห์ของเดการ์ต เพื่อพิจารณาปัญหาเกี่ยวกับเส้นสัมผัสเส้นโค้งผ่านทางปัญหาของการหารากซ้ำของสมการพหุนาม

ฮูดเด (Johann van Waveren Hudde, 1628 - 1704, the Netherlands) ได้ปรับปรุงวิธีการที่บัวเนอร์ใช้ ให้ง่ายลง จนได้เป็น กฎของฮูดเด (Hudde’s rule) โดยกฎนี้แสดงความสัมพันธ์ระหว่างรากซ้ำและสิ่งที่ต่อมาเรียกว่า อนุพันธ์ของฟังก์ชันพหุนาม

ทั้งระเบียบวิธีทางเรขาคณิตวิเคราะของเดการ์ตที่บัวเนอร์ใช้และกฎของฮูดเดได้มีส่วนสำคัญในการพัฒนาผลงานทางแคลคูลัสของนิวตัน

ไฮย์เคนส์ (Chistiaan Huygens, 1629 – 1695, Netherlands) มีผลงานที่เป็นแรงจูงใจให้ไลบ์นิตซ์พัฒนาแนวทางการเข้าถึงแนวคิดของแคลคูลัสได้ง่ายขึ้น

แบร์โรว์ (Isaac Barrow, 1630 – 1677, England) เป็นอีกบุคคลหนึ่งที่มีอิทธิพลต่อการพัฒนาผลงานของนักคณิตศาสตร์รุ่นถัดมาโดยเฉพาะไลบ์นิตซ์  แบร์โรว์เสนอระเบียบวิธีการพิจารณาเส้นสัมผัสเส้นโค้ง ว่าเป็น ลิมิตของลำดับของเส้นตัดเส้นโค้ง (secant lines) ตามที่ทราบกันแล้วในปัจจุบัน ซึ่งพอสังเขปแนวคิดนี้ได้ว่า

ถ้าเริ่มจากเส้นตัดเส้นโค้งเส้นหนึ่ง จะได้สองคู่อันดับของจุดตัดเหล่านั้นในระบบพิกัดฉาก  ให้สร้างเส้นตัดเส้นโค้งเส้นใหม่ซึ่งมีคู่อันดับของจุดตัดเส้นโค้งทั้งสอง โดยที่ค่าสัมบูรณ์ของผลต่างของพิกัดที่หนึ่งที่มีค่าน้อยกว่าเดิม ดำเนินกระบวนการสร้างนี้ไปเรื่อย ๆ โดยให้ค่าสัมบูรณ์ของผลต่างของพิกัดที่หนึ่งมีค่าเข้าใกล้ศูนย์ ในทางเรขาคณิตอาจถือได้ว่า กระบวนการสร้างนี้ให้ลำดับของเส้นตัดเส้นโค้งที่มีลักษณะใกล้เคียงกับเส้นสัมผ้สเส้นโค้งมากขึ้น (หากอาศัยแนวคิดของลิมิตที่ทราบแล้วในปัจจุบัน สามารถกล่าวได้ว่าเส้นลิมิตของเส้นตัดเส้นโค้งคือเส้นสัมผัสเส้นโค้ง )

มีความเป็นไปได้ว่าทั้งนิวตันและไลบ์นิตซ์ได้ศึกษาผลงานนี้และได้รับคำแนะนำจากแบร์โรว์ให้พัฒนาผลงานของตน 

บทพิสูจน์แสดงภาพแนวคิดของกระบวนการข้างบนหลายอัน มีรูปสามเหลี่ยมคล้ายๆ กับรูปด้านล่าง ซึ่งต่อมาเรียกชื่อว่า Barrow’s differential triangle  

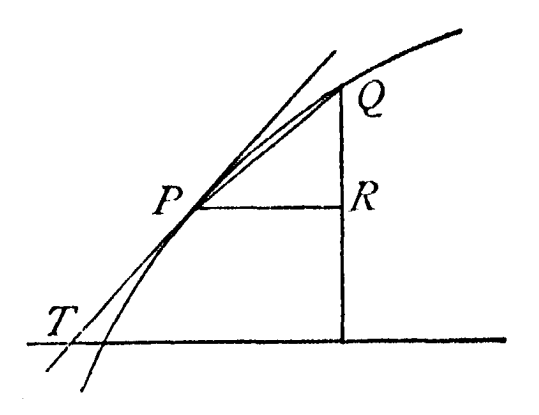
ผลงานชิ้นหนึ่งของ ปาสกาล(Blaise Pascal, 1623 – 1662, France) ก็มีรูปสามเหลี่ยมลักษณะเดียวกันที่เป็นแนวทางให้ไลบ์นิตซ์พัฒนาทฤษฎีบทของตัวเอง

ทั้งแบรโรว์และตรูริเชลลิ (Evangelista Torricelli, 1608 – 1647, Italy) ศึกษาปัญหาของการเคลื่อนที่ด้วยอัตราเร็วที่แปรผัน พบว่าการดำเนินการที่ต่อมาเรียกว่าอนุพันธ์ของระยะทางนี้ จะได้ความเร็ว และถ้าดำเนินการผกผันกระบวนการดังกล่าวจากความเร็วจะได้ระยะทาง แบร์โรว์รับรู้ถึงสองกระบวนการที่ผกผันซึ่งกันและกันซึ่ง (ต่อมาทราบกันว่าคือ อนุพันธ์และปริพันธ์ในแคลคูลัส) แต่ก็ไม่ได้ประโยชน์จากความรู้นี้มากนัก แต่ก็มีอิทธิพลให้นิวตันเสนอทฤษฎีบทหลักมูลของแคลคูลัสในเวลาต่อมา ในอีกทางหนึ่งผลงานเดียวกันของแบร์โรว์ บทพิสูจน์ที่เกี่ยวข้องกับ Barrow’s differential triangle ได้ให้แนวคิดแก่ไลบ์นิตซ์ในการประดิษฐ์สัญลักษณ์  

เพื่อแทนสิ่งที่สืบทอดมาจากชาวกรีกโบราณ นั่นคือ ขนาดที่แบ่งย่อยไม่ได้อีก และได้ให้กฎการดำเนินการเกี่ยวกับสัญลักษณ์เหล่านี้ ทำให้การศึกษาแนวคิดของแคลคูลัสทำได้ง่ายและสามารถต่อยอดออกไปอย่างที่เราได้ใช้อยู่ในปัจจุบัน

ยุคใหม่

นิวตัน ที่ได้ชื่อว่าเป็นผู้ก่อกำเนิดแคลคูลัสเพราะว่ามีผลงานที่สำคัญมากมายต่อการพัฒนารากฐานของแคลคูลัสดังจะเห็นได้จากผลงานที่รวบรวมไว้ในหนังสือชื่อชุด Principia  ตัวอย่างผลงานที่ได้กล่าวมาแล้วเช่น การเสนอทฤษฎีบทหลักมูลของแคลคูลัส เพื่อแสดงกระบวนการที่ผกผันกันของอนุพันธ์และปริพันธ์ตามที่แบร์โรว์ได้สังเกตเห็น โดยนิวตันได้ใช้ประโยชน์จากวิธีการนี้ในการแก้ปัญหาทางอนุพันธ์ (ซึ่งตอนนั้นเรียกว่า Method of tangents) และนำไปแก้ปัญหาทางปริพันธ์ (ซึ่งตอนนั้นเรียกว่า Method of quadrature)  

ในผลงาน Method of Fluxions ที่นิวตันได้ศึกษาเกี่ยวกับการเคลื่อนที่ มีการใช้แนวคิดของ ขนาดที่แบ่งย่อยไม่ได้อีก เช่นกัน ซึ่งนิวตันใช้สัญลักษณ์ 

แทน fluxion ของ x และ 

(ความเร่ง) แทน fluxion ของ fluxion  ของ x (เทียบได้กับอนุพันธ์อันดับหนึ่งและอนุพันธ์อันดับสองที่ทราบในปัจจุบัน) แต่ระบบการดำเนินการเกี่ยวกับสัญลักษณ์ที่นิวตัวใช้มีความคลุมเครือเข้าใจยากกว่าของระบบสัญลักษณ์ที่ไลบ์นิตซ์เสนอ  

ในผลงาน Tractatus de Quadratura Curvarum นิวตันได้ให้ระเบียบวิธีคิดเกี่ยวกับลิมิตเป็นศูนย์และการใช้อนุกรมกำลังแทนฟังก์ชันที่ทราบกันในปัจจุบัน

ไลบ์นิตซ์ นอกจากจะประดิษฐ์ระบบสัญลักษณ์ที่ใช้ง่ายกว่าสำหรับศึกษาแนวคิดของอนุพันธ์ (ตามแนวคิดที่ได้จากบทพิสูจน์ของแบร์โรว์ที่กล่าวแล้วข้างต้น) ยังประดิษฐ์ระบบสัญลักษณ์ที่ใช้แทนแนวคิดของปริพันธ์ โดยใช้

เป็นสัญลักษณ์แทนการบวกของ ขนาดที่แบ่งย่อยไม่ได้อีก  ดังที่ได้ระบุในระเบียบวิธีที่ คาวาลีเอรี เสนอ

ในผลงานชิ้นหนึ่ง ไลบ์นิตซ์ได้เขียนสมการ (ที่คุ้นเคยในปัจจุบัน) ได้แก่ 

เป็นจุดเริ่มต้นของแคลคูลัสเชิงปริพันธ์ ซึ่งสมัยนั้นไลบ์นิตซ์ใช้ชื่อว่า calculus summatorius หรือ calculus integralis 

ในเวลาต่อมา ระบบสัญลักษณ์ของอนุพันธ์และปริพันธ์ที่เสนอโดยไลบ์นิตซ์ได้รับความนิยมและใช้กัรอย่างแพร่หลาย ตามที่เห็นจนถึงปัจจุบัน

การพัฒนาแคลคูลัสในคริสต์ศักราชที่ 19 ยังอิงรากฐานทางคณิตศาสตร์จากผลงานที่สำคัญของนิวตันและไลบ์นิตซ์ มีทั้งที่อยู่บนความรู้

แบบสถิต (static phase) เช่น จากความรู้ในเรื่องการวัด แต่ยังมีการพัฒนาแคลคูลัสโดยอาศัยคณิตศาสตร์ของ infinitesimals ซึ่งตกทอดมาจากชาวกรีกโบราณ และสิ่งที่ปรับปรุงให้รัดกุมกว่าของคาวาลีเอรี ที่ชื่อ indivisible 

และอีกรากฐานบนความรู้แบบพลวัต (dynamic phase) เช่น การเคลื่อนที่ของจุดในปัญหาของเส้นสัมผัสเส้นโค้ง 

แต่ก็มีผู้ชี้ให้เห็นถึงจุดอ่อนของการให้เหตุผลทางตรรกในผลงานของนิวตันและไลบ์นิตซ์ เช่น เบอร์คเลย (George Berkeley, 1685 – 1753, England) จากผลงาน Analyst 

จากจุดนี้ทำให้แคลคูลัสต้องแสวงหารากฐานความรู้ที่รัดกุมกว่าเพื่อมารองรับแนวคิด ถือได้ว่าเป็นช่วงที่รากฐานของแคลคูลัสได้ขยับมาอยู่บนแขนงคณิตศาสตร์ที่เรียกว่า คณิตศาสตร์วิเคราะห์  

ผู้ที่มีบทบาทสำคัญในการเสนอความรู้ทางคณิตศาสตร์ที่จะเป็นรากฐานที่รัดกุมเข้มงวดกว่าให้กับแคลคูลัสคือ โคชี นักคณิตศาสตร์ชาวฝรั่งเศษนั่นเอง และความรู้ทางคณิตศาสตร์ที่เป็นรากฐานดังกล่าวคือ แนวคิดของลิมิตของฟังก์ชัน ซึ่งภายหลังได้มีบทนิยามของลิมิตของฟังก์ชันที่มีความรัดกุมยิ่งขึ้นอีก อย่างเช่น การเสนอให้เข้าถึงแนวคิดของลิมิตโดยใช้แนวคิดของ 

ซึ่งเสนอโดย ไวแยร์สตราสต์ (Karl Weierstrass, 1815 – 1897, Germany) 

และเชื่อว่ายังความจำเป็นพัฒนาแนวคิดของแคลคูลัสให้อยู่บนรากฐานแนวคิดของคณิตศาสตร์ที่สามารถให้เหตุผลได้รัดกุม เข้มงวด และขยายให้ครอบคลุมปัญหาต่างๆ ที่จะเกิดขึ้นจากความจำเป็นต้องพัฒนาความรู้ด้านวิทยาศาสตร์และวิศวกรรมศาสตร์ขั้นสูง เพื่อตอบสนองการแสวงหาความรู้ใหม่ของมนุนย์ ที่ไม่มีที่สิ้นสุด

อ้างอิง

• http://www.mscs.dal.ca/~kgardner/History.html
  
• http://en.wikipedia.org/wiki/Main_Page
  
• http://archive.org/details/historyofmathema031897mbp
  
• http://www.wolframalpha.com/
  
• http://www-history.mcs.st-and.ac.uk/HistTopics/The_rise_of_calculus.html
  
• The World of Mathematics by JAMES R. NEWMAN
  
• http://pages.bangor.ac.uk/~mas010/methmat.html
  
• http://www-history.mcs.st-and.ac.uk/Timelines/index.html