Space Venture

University of Nebraska- Lincoln Digital Commons - Honors Club

Space Venture

By: Mickey Tran Copyright 2018 by Mickey Tran under Creative Commons Non-Commercial License. Individuals and organizations may copy, reproduce, distribute, and perform this work and alter or remix this work for non-commercial purposes only.

Facilitator’s Guide
Space Venture is a set of challenges based on famous mathematical computational problems. The goal of this game is to introduce these different problems to kids through various scenarios. Space Venture can be played by all ages. 

Recommendations:
1st-5th grade level : simply allow the kids to play the game
6th grade level + : challenge the kids to find the most OPTIMAL solution whether it be the least amount of moves when SHIPPING or collecting the most items in EARTH SHELF. 

The instructions for each mission is on a card correlating to the board games itself. Each card will introduce the mission, give set up instructions, then tell players how the game will work. The end of each card will tell the kids the real life mathematical computational problem.
The following should already be included in the Space Venture Package: 

- 1 space venture title card
- 1 introduction card
- 1 facilitator’s guide
- 3 Mission Instruction cards & 3 Real Life explanations
- 1 Traveling Astronaut Board
- 1 Traveling Astronaut Score Marker
- 1 Earth Shelf Board
- 1 Earth items - NOT CUT OUT
- 1 Shipping Board
- 1 Shipping Score Marker

Introduction!

Welcome to Space Venture! You are an astronaut from the planet Earth. Other planets around the galaxy are running out of supplies; they need your help! The supplies are only found on Earth. You need to collect the supplies, map out a route to each planet, and deliver the supplies to teach planet. Complete all the challenges to save these planets!

Mission 1: Earth Shelf 

Players: 2 

Cut out the supplies on the paper or use real objects found around your area. 

Place the supplies on the ‘Earth Shelf’, using the number labled on the left corner of each shelf as a guide to the amount of items on each shelf. 

Players: Your first task is to collect the supplies on Earth! Lucky for you, there’s a station on Earth that has all the supplies you need. You are not the only astronaut on Earth! You must compete with other astronauts to get the supplies needed for the other planets. The station owner allows astronauts to take as many or few supplies on his shelf. BUT the station owner wants to keep one object on the shelf at all times. 

The first astronaut must choose a row on the shelf and can pick up as many or as few supplies as she wishes. Continue taking turns until an astronaut has to pick up the last object. Since the station owner wants one object on the shelf at all times, the astronaut who has to pick up the last object is kicked out of the store and winning astronaut gets all the supplies!

Shelf Image

Earth Shelf in Real Life: Nim’s Game

This challenge is based on a game called Nim’s game, where players must take turns removing blocks from a pile. The winner in this case is the person with the last block. Computer scientists and mathematicians use this game to find a pattern in choosing the number of blocks you may take. It’s an exponential growth pattern that uses the power of twos. 

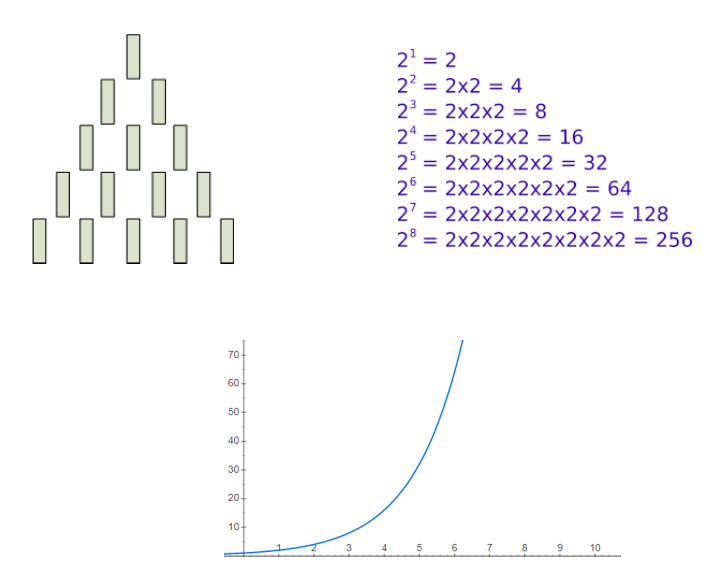
Nims Game Illustrated

Space Shelf

Earth Supply cards

Mission 2: Traveling Astronaut Challenge other players to find the shortest path. Player with the smallest path wins!

 Players: 1+ 

You have your supplies! Unfortunately, your rocketship is limited on rocket fuel. You must find the shortest way to travel to all the planets and back to Earth before your rocket runs out of fuel. Use the map provided to find the shortest route. You cannot revisit a planet once you have chosen to go to that planet. Calculate your route by adding the paths you chose and putting it in the ‘Sum’ box. 

Mission 2 image

Traveling Astronaut in Real Life: Traveling Salesman 

This is based off of a famous math problem called the ‘Traveling Salesman’. The goal is to optimize or find the best route for the salesman to take as he travels to each city. Best route may mean fastest and shortest path. Each city is represented by a node or dot. To solve this problem, scientists draw out graphs. This problem is known to be very difficult to solve in the world of computation because it can take a very long time to answer the more cities you add. 

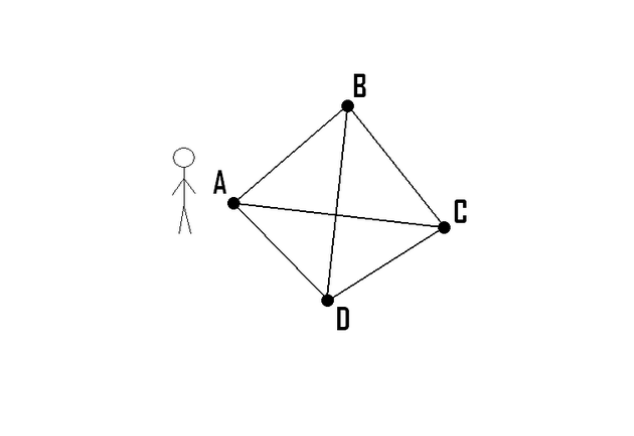
Traveling Salesman example

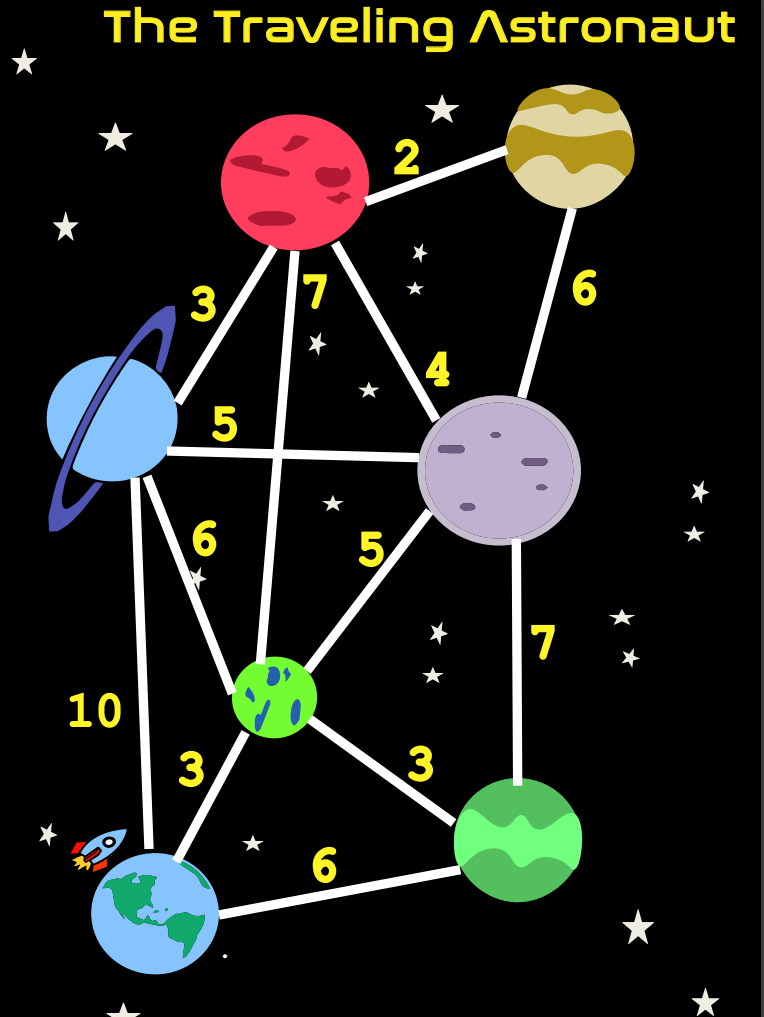
Traveling Astronaut

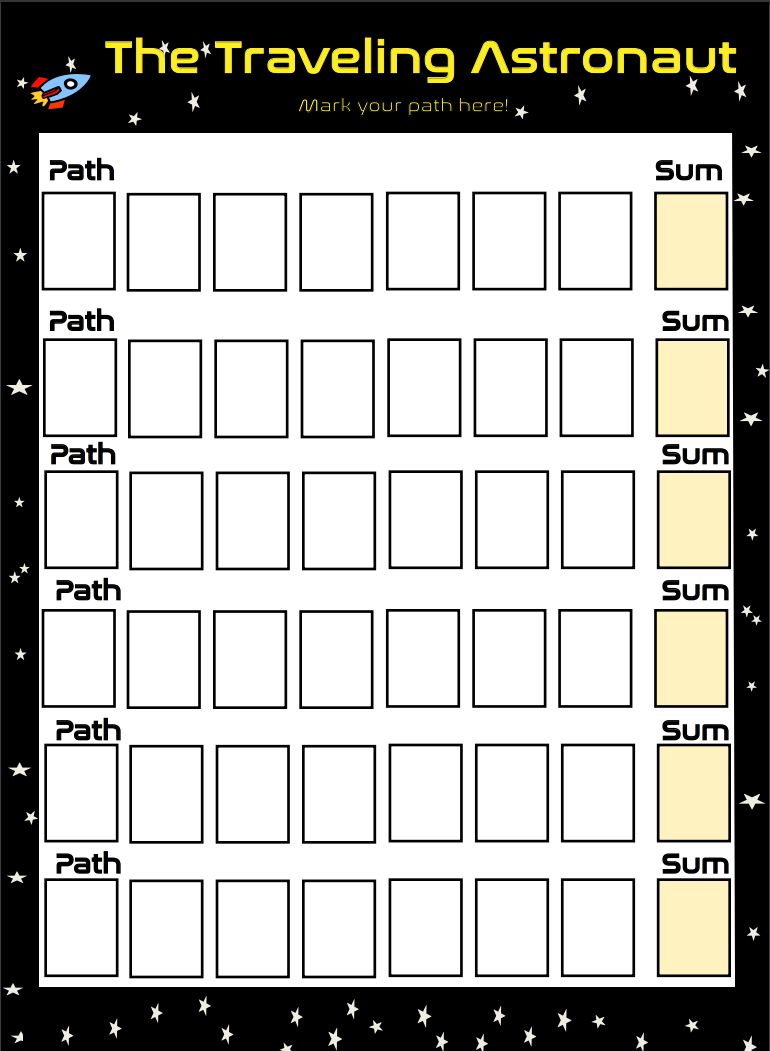
Traveling astronaut worksheet

Mission 3: Shipping 

Cut and fold out the box templates.
There are 3 different boxes of different sizes : small, medium, and large.
Put 8 supplies in the large box.
Put 5 supplies in the medium box.
Put 3 supplies in the small box.
Heavier objects should be placed in the large box, while lightest objects be placed in the small box. 

Players: 1+ 

The large box is the heaviest. The medium box is the second heaviest. The small box is the lightest.
The boxes must be stacked on top of another from heaviest to lightest.
Only ONE box can be moved at a time. Each time a box is placed in a different slot it counts as 1 move.
The smaller boxes are delicate so the heavier boxes cannot be put on top of them.
To deliver these boxes you must go back and forth between Earth, the rocketship, and the planets (slot 1, slot 2, slot 3).
On the board, you will place the stacked boxes one slot 1 to begin.
The goal is to get all the boxes over to the planets (slot 3) stacked from heaviest to lightest.
Try to get all the boxes over to the planets in 7 MOVES!

Shipping in Real Life: Tower of Hanoi 

This challenge comes from the famous ‘Tower of Hanoi’ problem given to computer scientists. There is a pattern that can be found when trying to find the least amount of moves in stacking these boxes and other amounts of boxes. Through this pattern, computer scientists found they could use recursion or a pattern that uses information from one step to find the next.

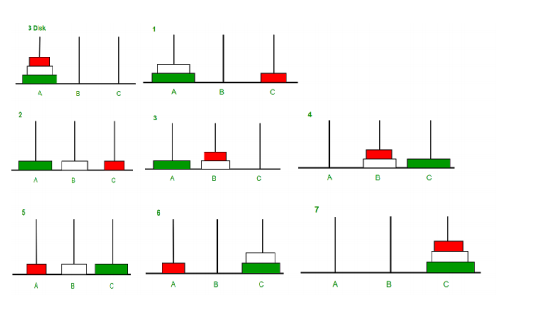
Tower Of Hanoi Example

Move Marker Worksheet

Shipping Mission1

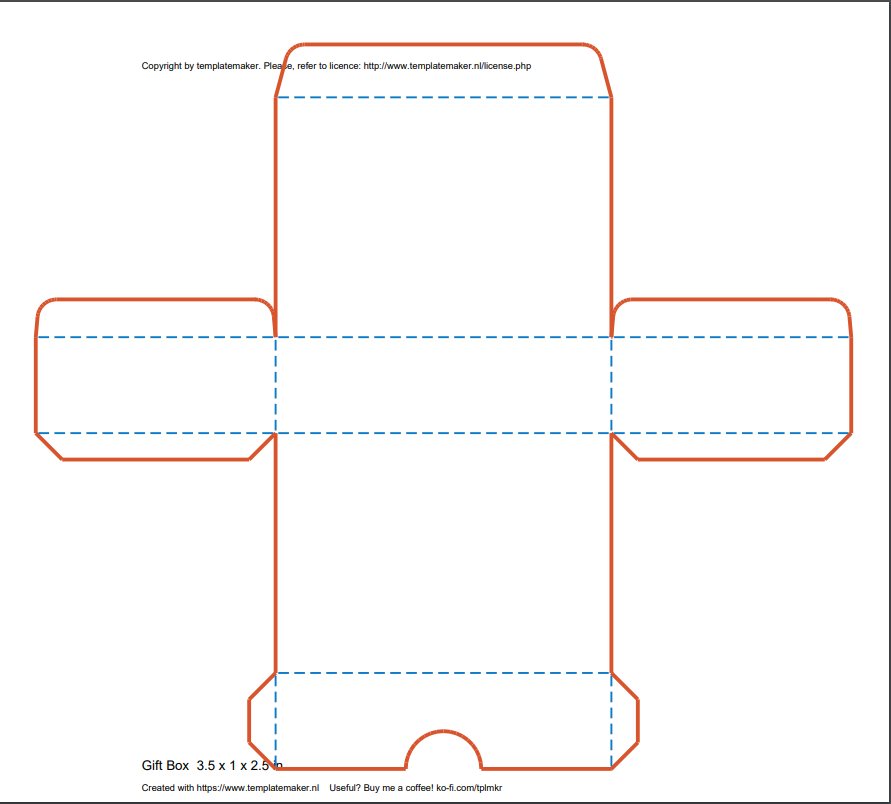
Box 1 template

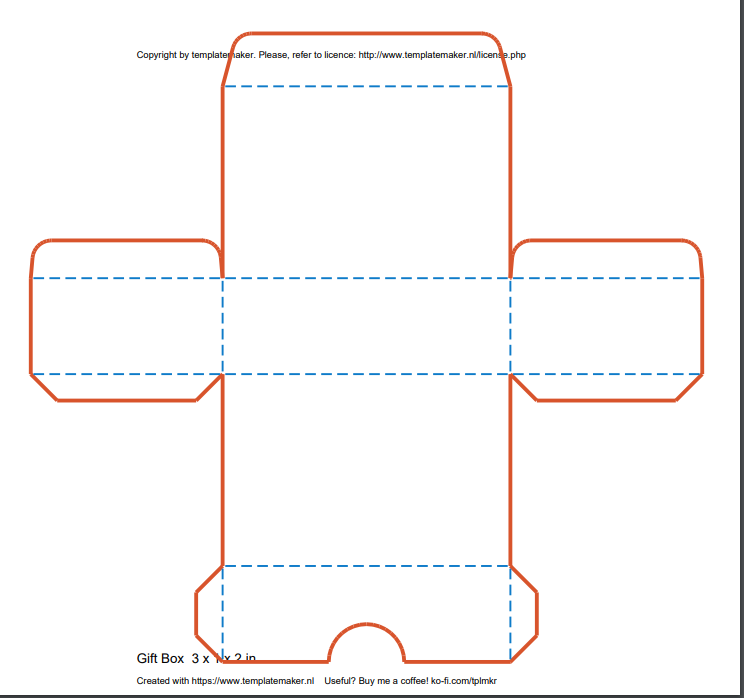
Box 2 template

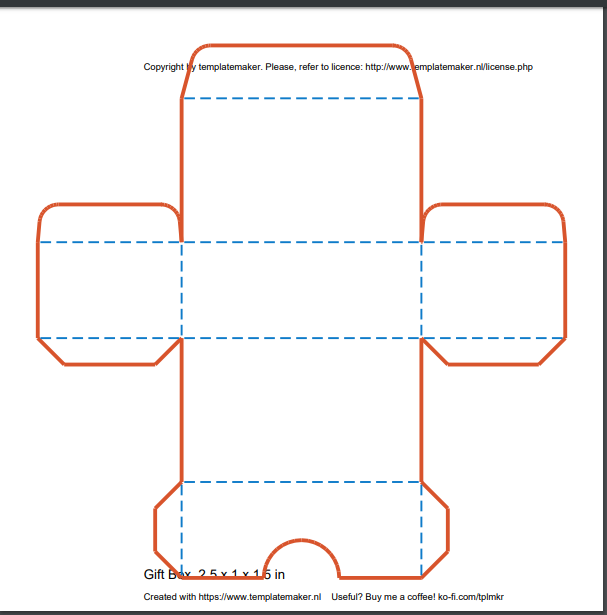
Box 3 Template