3.MD.C.7d Area & 3.MD.D.8 Perimeter of a Rectilinear Figure-Dog Park REMIX

3.MD.C.7d Area & 3.MD.D.8 Perimeter of a Rectilinear Figure (Concrete Referents)

Evidence Statement 3.C.3-2- Base explanations/reasoning on concrete referents such as diagrams (whether provided in the prompt or constructed by the student in their response), connecting the diagrams to a written (symbolic) method.

The Dog Park

A model of a dog park is shown.

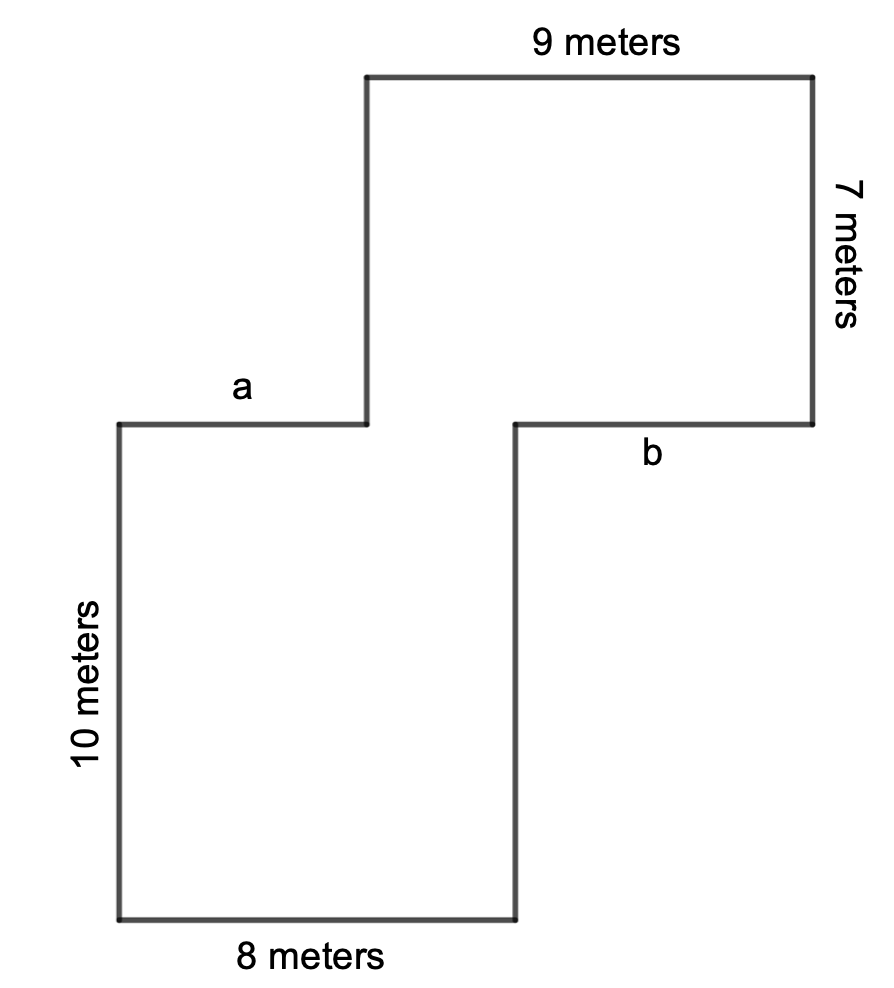
Can the area and perimeter of this dog park be found?

1. Find the area, in square meters, of the dog park. 

2. Support your answer to item (1) using an equation or equations. 

3. Explain why you cannot find the perimeter, in meters, of the dog park. What other information is needed to find the perimeter of the dog park? 

4. Given the diagram of the dog park, label the diagram with exactly one more measurement (either (a) or (b)) to find the perimeter of the dog park. (You can choose your number. What number do you choose?) Now find the perimeter of the dog park. 

5. Why is it okay to only give one more measurement for either (a) or (b)? Give an equation, equations, or an explanation to support your answer. 

Consider a second model of a dog park.

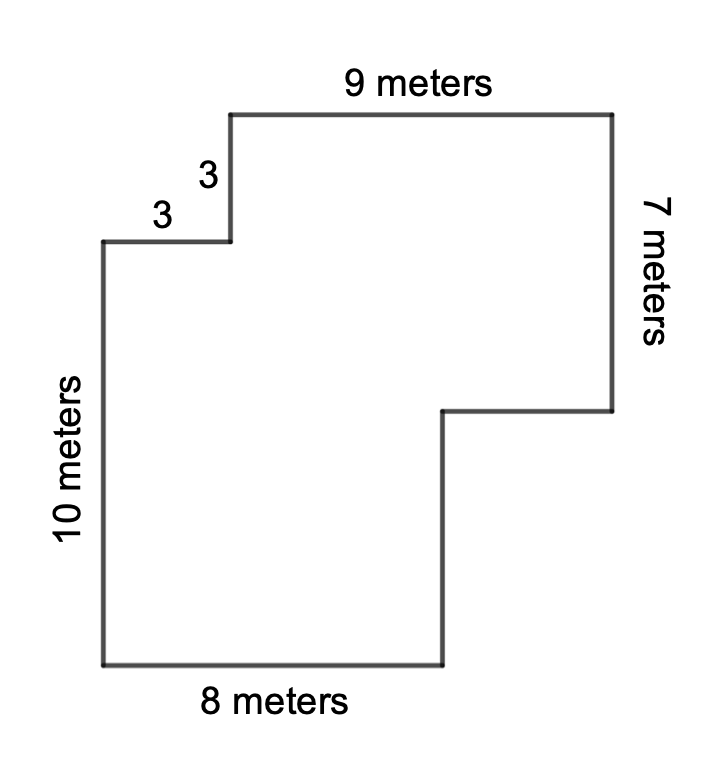
Can the perimeter and area of this dog park be found?

6. Find the perimeter, in meters, of this second dog park.

7. Support your answer to item (6) using an equation or equations. 

8. Find the area, in square meters, of the second dog park.

9. Support your answer to item (8) using an equation or equations.

10. Consider a second way to find the area of the dog park.

11. Support your answer to item (10) using an equation or equations.

12. Compare your methods with at least two other students. How many different ways were used to find the area of the dog park?

Scoring Rubric

Score of 3 Points

Student response includes each of the following 3 elements.

·      Computation component- identifies the correct area of 143 square meters.

·      Modeling component: Provides equations showing how to find the area of the two different sections of the dog park.

·      Modeling component- Provides an equation to find the total area of the playground.     

·      Sample Student Response: The area of the dog park is 143 square meters. I found the area of the two sections of the dog park: 7 x 9 = 63 and 8 x 10 = 80. If you add the area of the two rectangles, you will find the area of the entire dog park. 63 + 80 = 143.

·      Student identifies that not enough information is given in the diagram, that the length of side (a) or side (b) is needed to determine the perimeter.

·      Students chooses a measurement for either (a) or (b). If (a) is known, then (b) must be 9 – (8 – a) = 1 + a. If (b) is known, then (a) can be found by (8 – (9 – b)) = b-1. Students should choose (a) to be between 0 and 8, or (b) to be between 0 and 9.  

·      For the second dog park, students should identify that given the lengths of the sides labeled with 3 meters, they can find the lengths of the two remaining sides. They will likely draw additional segments to show the overlapping portions of the rectangles, seeing that the 8x10 rectangle overlaps the 9x7 rectangle with a rectangle measuring 5x4 (horizontal x vertical).

·      Once the lengths of the overlapping portions of the rectangles are identified, students can determine both the perimeter and the area of the dog park.

·      The area of the dog park can be found by partitioning the region into multiple rectangles or by considering the area of a large rectangle containing the whole park and then subtracting the areas of rectangles that can be removed from the larger rectangle.

Notes: labeling the answer with square meters is not requires. However, if the student provides and incorrect label, the student cannot earn a score of 3 points.

Score of 2 Points

Student response includes 6 of the 9 elements. Or, the student does not compute the correct total area(s) or perimeter(s) due to a computation error but provides a valid strategy and equations.

Score of 1 Point

Student response includes 3 of the 9 elements.

Score of 0 Points

Student response is incorrect or irrelevant.