Goals and Learning ObjectivesFind the least common multiple of two whole numbers equal to or less than 12.
In this lesson, students apply what they have learned about factors and multiples to solve a variety of problems. In the first activity, students to use what they have learned about common factors and common multiples to solve less structured problems in context (MP1).
Students will learn to use the distributive property to rewrite each sum as a product. Visual representations of the areas of rectangles and their respective measurements (length and width) will be used.
Student can transfer between fractions, decimals, and percents.
Recognize equivalent forms of rational numbers.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Seth wants to buy a new skateboard that costs \$167. He has \$88 in the bank. If he earns \$7.25 an hour pulling weeds, how many hours will Seth have t...
This is the first of two lessons that develop the idea of equivalent ratios.
In this lesson, they work with equivalent ratios more abstractly, both in the context of recipes and in the context of abstract ratios of numbers. They understand and articulate that all ratios that are equivalent to a:b can be generated by multiplying both aand b by the same number (MP6).By connecting concrete quantitative experiences to abstract representations that are independent of a context, students develop their skills in reasoning abstractly and quantitatively (MP2). They continue to use diagrams, words, or a combination of both for their explanations. The goal in subsequent lessons is to develop a general definition of equivalent ratios.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
In this lesson, students use collections of objects to make sense of and use ratio language. Students see that there are several different ways to describe a situation using ratio language. For example, if we have 12 squares and 4 circles, we can say the ratio of squares to circles is 12:4 and the ratio of circles to squares is 4 to 12. We may also see a structure that prompts us to regroup them and say that there are 6 squares for every 2 circles, or 3 squares for every one circle (MP7).Expressing associations of quantities in a context—as students will be doing in this lesson—requires students to use ratio language with care (MP6). Making groups of physical objects that correspond with “for every” language is a concrete way for students to make sense of the problem (MP1).
Students work with a set of cards showing different ways of expressing ratios, including both part-part statements and part-whole statements. They group the cards that show the same ratio of boys to girls, but without the explicit use of the term equivalent.Key ConceptsRatios can be represented in a:b form, as fractions, as decimals, as factors, and in words; they can be expressed in part-part statements or in part-whole statements.Goals and Learning ObjectivesGroup cards showing ratios that are equivalent but expressed in different forms.
Solve problems involving ratios and rates.
a. Create tables of equivalent ratios, find missing values in the tables and plot the pairs of values on the Cartesian coordinate plane.
b. Solve unit rate problems.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
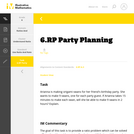
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
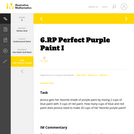
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
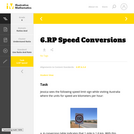
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
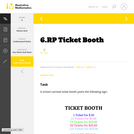
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.