OREGON MATH STANDARDS (2021): [4.GM]
![OREGON MATH STANDARDS (2021): [4.GM]](https://img.oercommons.org/780x780/oercommons/media/courseware/lesson/image/13138_ODE_Math_Logo_2018-H_color_BvjqVNy.png)
Overview
The intent of clarifying statements is to provide additional guidance for educators to communicate the intent of the standard to support the future development of curricular resources and assessments aligned to the 2021 math standards.
Clarifying statements can be in the form of succinct sentences or paragraphs that attend to one of four types of clarifications: (1) Student Experiences; (2) Examples; (3) Boundaries; and (4) Connection to Math Practices.
2021 Oregon Math Guidance: 4.GM.A.1
Cluster: 4.GM.A - Draw and identify lines and angles, and classify shapes by properties of their lines and angles.
STANDARD: 4.GM.A.1
 Standards Statement (2021):
Standards Statement (2021):
Explore, investigate, and draw points, lines, line segments, rays, angles, and perpendicular and parallel lines. Identify these in two-dimensional figures.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
3.GM.A.1 | 4.GM.A.2, 4.GM.C.7, HS.GM.A.4 | N/A | 4.G.A.1 4.GM.A Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- Students should draw points, lines, line segments, rays, angles (right, acute, and obtuse), and perpendicular lines.
- Expectation that drawing and identifying right, acute, and obtuse angles are included in this standard.
Terminology
- Right angle – An angle measuring exactly 90°.
- Acute angle – An angle larger than 0° and smaller than 90°.
- Obtuse angle – An angle larger than 90° and smaller than 180°.
- Perpendicular lines – Two lines that meet to form an intersection at a right angle
Teaching Strategies
- Students should investigate lines of symmetry in two dimensional figures as a property. This is an extension from work in third grade.
Progressions
- Students see points and lines as abstract objects: Lines are infinite in extent and points have location but no dimension. Grids are made of points and lines and do not end at the edge of the paper. (Please reference page 15 in the Progression document).
Examples
- How many lines of symmetry do each of the quadrilaterals to the right have?
- Illustrative Mathematics:
2021 Oregon Math Guidance: 4.GM.A.2
Cluster: 4.GM.A - Draw and identify lines and angles, and classify shapes by properties of their lines and angles.
STANDARD: 4.GM.A.2
 Standards Statement (2021):
Standards Statement (2021):
Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
4.GM.A.1, 4.GM.C.7 | 5.GM.B.3, 5.GM.D.6, HS.GM.A.4 | N/A | 4.G.A.2 4.GM.A Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- Right angles should be indicated with a square symbol.
- Polygons should include triangles, quadrilaterals including kites, trapezoids, rectangles, squares, rhombuses, and other parallelograms, and pentagons.
Terminology
- A polygon is a closed figure with at least three straight sides and angles; a polygon is regular only when all sides are equal and all angles are equal; and a polygon is irregular when all sides are not equal or all angles are not equal.
- Isosceles triangle – A triangle containing at least two equal length sides and two equal interior angle measures. Sub- class includes equilateral triangles.
- Equilateral triangle – A triangle with three equal-length sides and three 60-degree interior angles. Also known as an equiangular triangle.
- Scalene triangle – A triangle containing three unequal side lengths and three unequal angle measures.
- Right triangle – a triangle with one right angle.
- Acute triangle – a triangle containing three acute angles.
- Obtuse triangle – a triangle containing one obtuse angle.
Boundaries
- This objective does not require students to create a hierarchy.
Progressions
- Students can use side length to classify triangles as equilateral, equiangular, isosceles, or scalene; and can use angle size to classify them as acute, right, or obtuse. They then learn to cross-classify, for example, naming a shape as a right isosceles triangle. Thus, students develop explicit awareness of and vocabulary for many concepts they have been developing, including points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. (Please reference page 15 in the Progression document).
Examples
- Illustrative Mathematics:
- Student Achievement Partners:
2021 Oregon Math Guidance: 4.GM.A.3
Cluster: 4.GM.A - Draw and identify lines and angles, and classify shapes by properties of their lines and angles.
STANDARD: 4.GM.A.3
 Standards Statement (2021):
Standards Statement (2021):
Recognize and draw a line of symmetry for a two dimensional figure.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
1.GM.A.2 | HS.GM.A.4 | N/A | 4.G.A.3 4.GM.A Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- A line of symmetry is a line across the figure such that the figure can be folded along the line into matching parts.
Teaching Strategies
- Students should be provided multiple opportunities to investigate symmetry through paper folding and/or the use of mirrors.
- Students should develop an understanding of what a line of symmetry is through exploration with real-world objects.
- Identify or create line-symmetric figures by drawing and testing proposed lines of symmetry and sketching the second half of a symmetrical figure. (MP.7)
Examples
- Identify lines of symmetry seen in real-life objects, such as a butterfly, stop sign, flower, or dragonfly. Identify lines of symmetry seen and how they connect to the object.
- Illustrative Mathematics:
- Student Achievement Partners:
2021 Oregon Math Guidance: 4.GM.B.4
Cluster: 4.GM.B - Solve problems involving measurement and conversion of measurements.
STANDARD: 4.GM.B.4
 Standards Statement (2021):
Standards Statement (2021):
Know relative sizes of measurement units and express measurements in a larger unit in terms of a smaller unit.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
2.GM.D.11, 3.GM.B.4 | 4.GM.B.5, 5.GM.C.4 | 3.OA.C.7, 6.RP.A.1 | 4.MD.A.1 4.GM.B Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- Students can convert within a single system of measurement, express measurements in a larger unit in terms of a smaller unit.
- Students can record measurement equivalents in a two-column table.
Boundaries
- Measurement units within one system a student should be familiar with include km, m, cm, kg, g, lb, oz, l, hr, min, sec.
- Instruction could familiarity of like units in different measurement systems, but does not need to include formal conversions between similar units (e.g. kilometer (km) and miles (mi), kilograms (kg) and pounds (lb), liters (l) to gallons (g), etc.)
Progressions
- Justify conversions using understanding that larger units can be partitioned into smaller equal sized units (MP.3)
- Relating units within the metric system is another opportunity to think about place value. For example, students might make a table that shows measurements of the same lengths in centimeters and meters. (Please reference page 20 in the Progression document).
Examples
- Know that 1 ft is 12 times as long as 1 in. Express the length of a 4 ft. snake as 48 inches. Generate a conversion table for feet and inches listed as number pairs (1, 12), (2, 24), (3, 36), ….
- Illustrative Mathematics:
- Student Achievement Partners:
2021 Oregon Math Guidance: 4.GM.B.5
Cluster: 4.GM.B - Solve problems involving measurement and conversion of measurements.
STANDARD: 4.GM.B.5
 Standards Statement (2021):
Standards Statement (2021):
Apply knowledge of the four operations and relative size of measurement units to solve problems in authentic contexts that include familiar fractions or decimals.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
4.GM.B.4 | 5.GM.C.4 | 4.OA.A.3, 4.NF.B.3, 4.NF.B.4, 4.NF.C.5, 4.NF.C.6, 5.NF.B.3, 5.NF.B.5, 5.NF.B.6 | 4.MD.A.2 4.GM.B Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- Students should express larger units in terms of smaller units within the same measurement system
- Students should express smaller units in terms of larger units within the same measurement system.
- Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.
- Student should experience problems involving distances, intervals of time, liquid volumes, masses of objects, and money.
Terminology
- Metric measurement units include weight (grams and kilograms) capacity (milliliters and liters), length (centimeter, meter, and kilometer).
Boundaries
- Word problems should involve simple fractions or decimals and expressing measurements given in a larger unit in terms of a smaller unit.
- Fractions should be limited to denominators of 2, 3, 4, 5, 6, 8, 10, 12, and 100.
- Multiplication and division of fractions is not a requirement of this grade level.
- Contexts could include distance, intervals of time, liquid volumes, mass and money.
Teaching Strategies
- Represent measurement quantities using number line diagrams that feature a measurement scale.
- Students should reason about the relative sizes of measurement units within the metric system.
- Students should be able to accurately record measurement equivalents in a two-column table.
Progressions
- Students combine competencies from different domains as they solve measurement problems using all four arithmetic operations: addition, subtraction, multiplication, and division. For example, “How many liters of juice does the class need to have at least 35 cups if each cup takes 225 ml?” Students may use tape or number line diagrams for solving such problems (MP1). (Please reference page 20 in the Progression document).
Examples
- What time does Eric have to leave his house to get to the concert by quarter after nine, if the trip takes 90 minutes?
- Illustrative Mathematics:
2021 Oregon Math Guidance: 4.GM.B.6
Cluster: 4.GM.B - Solve problems involving measurement and conversion of measurements.
STANDARD: 4.GM.B.6
 Standards Statement (2021):
Standards Statement (2021):
Apply the area and perimeter formulas for rectangles in authentic contexts and mathematical problems.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
3.GM.C.7, 3.GM.D.8 | 6.GM.A.1 | 3.OA.A.4 | 4.MD.A.3 4.GM.B Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- Students should express their answers in linear (perimeter) and square (area) units. Students are not expected to use the 1 𝑐𝑚2 notation.
Boundaries
- Students should not be expected to find unknown side lengths when exploring composite rectangles.
Progressions
- Such abstraction and use of formulas underscores the importance of distinguishing between area and perimeter in Grade 3 (3.MD.8 3) and maintaining the distinction in Grade 4 and later grades, where rectangle perimeter and area problems may get more complex and problem solving can benefit from knowing or being able to rapidly remind oneself of how to find an area or perimeter.
- By repeatedly reasoning about how to calculate areas and perimeters of rectangles, students can come to see area and perimeter formulas as summaries of all such calculations (MP8). (Please reference page 21 in the Progression document)
Examples
- Find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
- Illustrative Mathematics:
2021 Oregon Math Guidance: 4.GM.C.7
Cluster: 4.GM.C - Geometric measurement: understand concepts of angle and measure angles.
STANDARD: 4.GM.C.7
 Standards Statement (2021):
Standards Statement (2021):
Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint. Understand and apply concepts of angle measurement.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
4.GM.A.1 | 4.GM.A.2, 4.GM.C.8, 4.GM.C.9, 7.GM.B.4, HS.GM.A.4 | N/A | 4.MD.C.5 4.GM.C Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- An angle can be viewed as a wedge of a circle or a turn through a circular arc where 1/360 of the wedge or turn is one-degree.
- An angle that turns through n one-degree angles is said to have an angle measure of n degrees.
- Draw right, acute, and obtuse angles
Teaching Strategies
- Students should also be able to explore this learning objective in the context of angles within circles.
- Angle measurement should be introduced with non- standard tools such as pattern blocks, unit angles, and/or wedges prior to introducing protractors. 360-degree protractors would make an explicit connection to the degrees of a circle and builds conceptual understanding of angles.
Progressions
- As with length, area, and volume, students need to understand equal partitioning and unit iteration to understand angle and turn measure. Whether defined as more statically as the measure of the figure formed by the intersection of two rays or as turning, having a given angle measure involves a relationship between components of plane figures and therefore is a property. (Please reference page 23 in the Progression document).
Examples
- The student can place four squares around the center of a circle. Since there are 360 degrees in a circle, 360 ÷ 4 = 90, so each square has 90-degree angles.
- Student Achievement Partners:
2021 Oregon Math Guidance: 4.GM.C.8
Cluster: 4.GM.C - Geometric measurement: understand concepts of angle and measure angles.
STANDARD: 4.GM.C.8
 Standards Statement (2021):
Standards Statement (2021):
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
4.GM.C.7 | 4.GM.C.9 | N/A | 4.MD.C.6 4.GM.C Crosswalk |
 Standards Guidance:
Standards Guidance:
Clarifications
- To understand measurement, students should measure in non-standard units, such as unit angles or wedges, before being introduced to tools with abstract units such as degrees.
Teaching Strategies
- Use angle measurement tools that help students connect non-standard units (wedges, unit angles, etc.) to standard units of angle measurement (degrees).
Progressions
- If examples and tasks are not varied, students can develop incomplete and inaccurate notions. For example, some come to associate all slanted lines with 45 degree measures and horizontal and vertical lines with measures of 90 degrees. Others believe angles can be “read off” a protractor in “standard” position, that is, a base is horizontal, even if neither arm of the angle is horizontal. Measuring and then sketching many angles with no horizontal or vertical arms, perhaps initially using circular 360 protractors, can help students avoid such limited conceptions. (Please reference page 23 in the Progression document).
Examples
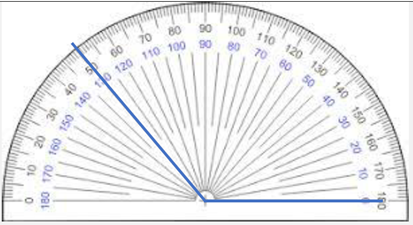
- Students may be given angles to find precise measurements of angles. Here are some examples of how students may use protractors and measurement reasoning to determine precise angle measurements.
- Sample student response: The angle is an obtuse angle because it is open more than a square corner angle. It measures 130 degrees.
- Illustrative Mathematics:
2021 Oregon Math Guidance: 4.GM.C.9
Cluster: 4.GM.C - Geometric measurement: understand concepts of angle and measure angles.
STANDARD: 4.GM.C.9
 Standards Statement (2021):
Standards Statement (2021):
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts.
 Connections:
Connections:
Preceding Pathway Content (2021) | Subsequent Pathway Content (2021) | Cross Domain Connections (2021) | Common Core (CCSS) (2010) |
4.GM.C.7, 4.GM.C.8 | 7.GM.B.4 | N/A | 4.MD.C.7 4.GM.C Crosswalk |
 Standards Guidance:
Standards Guidance:
Boundaries
- Expectation includes solving addition and subtraction problems to find unknown angles on a diagram in authentic contexts and mathematical problems such as by using an equation with a symbol for the unknown angle measure.
Progressions
- Students with an accurate conception of angle can recognize that angle measure is additive. As with length, area, and volume, when an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Students can then solve interesting and challenging addition and subtraction problems to find the measurements of unknown angles on a diagram in real world and mathematical problems. (Please reference page 24 in the Progression document).
Examples
- Using an equation with a symbol for the unknown angle measure.
- Illustrative Mathematics:
- Student Achievement Partners: