- Author:
- Bonnie Waltz, Deanna Mayers, Tracy Rains
- Subject:
- Mathematics, Algebra
- Material Type:
- Lesson Plan
- Level:
- High School
- Grade:
- 9, 10, 11, 12
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Interactive, Text/HTML, Video
Common Course Cartridge
The Pythagorean Theorem
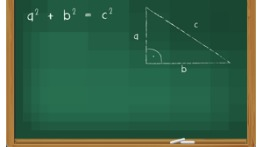
Overview
This seminar will teach you about the Pythagorean Theorem. It will also teach you how to use the converse of the theorem and how to identify Pythagorean triples. You will have to apply the techniques you have learned to simplify radicals, and you will learn how to apply exponential properties. You will be shown visual demonstrations of the Pythagorean Theorem and be asked to connect them to the algebraic models of the Theorem.
Standards
CC.2.3.8.A.3.
Understand and apply the Pythagorean Theorem to solve problems.
Engage
Introductory warm-up activity.
You are in charge of ordering pizza for a party. The restaurant has three different sizes of pizza which can be represented by each of the squares in the figure above. You can choose to buy either one “c” pizza (the pink square), OR you can buy both an “a” and a “b” pizza (the green and yellow squares). Which choice do you think would give you more pizza? How did you arrive at your conjecture?
Explore
Read or watch the resources to learn about this concept, then do the practice activity.
Read | Watch | Do |
Read the lesson “The Pythagorean Theorem” from the Monterey Institute. The information in this reading will show you how to solve problems using the Pythagorean Theorem. Be sure to work through all of the example problems that are included in the article. | Watch the video Algebra - Pythagorean Theorem in order to learn how to solve various types of problems using the Pythagorean Theorem. As you watch the video, practice with the problems found here. | Navigate through the Quizlet activity in order to practice solving problems using the Pythagorean Theorem. Be sure to complete each activity. |
Explain
Discuss your ideas / opinions / understandings.
Answer the following questions using complete sentences.
When using the Pythagorean Theorem to find missing side lengths in a right triangle, when would it be useful to leave answers in radical form? When would it be useful to round answers to a specific decimal place?
Explain how the Pythagorean Theorem could be used to determine whether the corner of a room forms a perfect right angle.
Evaluate
Now it is time to self-check how much you have learned about the this topic. If you do not know as much as you thought, go back to the “Explore” section of this seminar and reread, rewatch, or redo the activities listed. See your facilitator if you have questions.
Click here to take the quiz online. You do not have to log into the quiz site in order to take this quiz. If a window pops up asking you to sign up for the quiz site, just close the sign-up window and start your quiz.
Elaborate
This is a task or project where you can show what you know.
Directions:
Consider the right triangle shown below.
Compare the area of the largest semicircle to the areas of the two smaller semicircles. What is the relationship between the areas? How does this relate to the Pythagorean Theorem? Verify your results and conjectures by substituting three sets of Pythagorean triples into your expressions and comparing your simplified results. Use algebraic calculations and geometric formulas to justify your results, and be sure to answer all questions in complete sentences.
Points Possible | Points Earned | |
Formulas are correctly derived and compared, and Pythagorean triples are correctly used for justification of conjectures | 30 | |
Mathematical connections are expressed thoughtfully and completely | 30 | |
Questions are answered thoroughly and using complete sentences | 30 | |
Total | 90 |
Express
Complete this wrap-up activity where you reflect on your learning.
Imagine that a classmate tells you during a lesson on the Pythagorean Theorem that he doesn’t understand why the class has to learn about triangles during an algebra class. What would you tell him? Do you agree or disagree with him? Why?