6.NS.B.2 Lesson 2

Overview
Students review the standard long-division algorithm and discuss the different ways the answer to a whole-number division problem can be expressed (as a whole number plus a remainder, as a mixed number, or as a decimal).
Students solve a series of real-world problems that require the same whole number division operation, but have different answers because of how the remainder is interpreted.
Key Concepts
Students have been dividing multidigit whole numbers since Grade 4. By the end of Grade 6, they are expected to be fluent with the standard long-division algorithm. In this lesson, this algorithm is reviewed along with the various ways of expressing the answer to a long division problem. Students will have more opportunities to practice the algorithm in the Exercises.
Goals and Learning Objectives
- Review and practice the standard long-division algorithm.
- Answer a real-world word problem that involves division in a way that makes sense in the context of the problem.
Warm Up - Number Talk: Estimating Quotients
This number talk prompts students to make reasonable estimates of quotients using their knowledge of numbers, division, and structures. Only two problems are given to allow more time for students to share their estimation strategies.
Making reasonable estimates helps to develop arithmetic fluency. Here, it relies on understanding the relationship between multiplication and division, and on the different properties of operations (commutative, associative, and distributive). For example, to find 500÷7, students might think of the multiplication equation 7⋅?=500. Since they know that 7⋅100=700 and 7⋅30=210, and that 500=700−200, they could reason that 500 would be approximately 7⋅(100−30) or 7⋅70.
Launch
Display each problem one at a time for all to see. Give students 1 minute of quiet think time and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Support for Students with Disabilities
Memory: Processing Time. Provide sticky notes or mini whiteboards to aid students with working memory challenges.
Student Response
Answers vary. Sample responses:
- 70, because 7⋅7=49, so 70⋅7=490, which is almost 500.
- 150, because 100⋅9=900 and 50⋅9=450, so 150⋅9=1,350.
Anticipated Misconceptions
Students might try to calculate exact answers and take longer to produce an answer. Encourage them to approximate the actual answer by rounding the dividend or divisor or starting with friendlier numbers.
Activity Synthesis
Invite students to share their strategies. Record and display student explanations for all to see. Ask students to explain if or how the dividend or divisor impacted their choice of strategy. To involve more students in the conversation, consider asking:
- “Did anyone reason about the problem the same way but would explain it differently?”
- “Did anyone estimate in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
- “Do you agree or disagree? Why?”
At the end of the discussion, if time permits, ask a few students to share a story problem or context that 1,394÷9 could represent.
Estimate these quotients mentally.
500 ÷ 7
1,394 ÷ 9
Compare Solutions
Lesson Guide
Give students a few minutes to discuss the question with a partner; then have students share their ideas with the class.
SWD: Consider the prerequisite skills for this lesson. Students with disabilities may need review, direct instruction, and guided practice with the skills needed to complete the tasks that follow. Make sure all students understand how to divide multidigit whole numbers. If students are unclear, pull a small group and pre-teach the students who are unsure.
Mathematics
Review how the standard algorithm is used to find the quotient in the opening. You might ask students to tell you what to do at each step.






Jason, Denzel, and Martin are all correct. Here is how 172 R8 is equivalent to 172 and 172.25:
- The answer 172 R8 means that when we divide 5,512 into 32 groups, we get groups of 172 with 8 left over.
- If we divide the leftover 8 into 32 groups, there will be another , or , in each group. So, the quotient is 172, (172 + ), or 172.25.
Opening
Compare Solutions
Jason, Denzel, and Martin solved the division problem 5,512 ÷ 32.
All three students started out using the steps shown, but all three got different answers.
Here are their answers:
Jason’s answer: 172 R8
Denzel’s answer: 172
Martin’s answer: 172.25
- Which answer is correct, and why?
- Discuss this question with your partner, and then with your class.

Analyze Using Long Division to Calculate Quotients with Remainder
In this activity, students use long division to divide whole numbers whose quotient is not a whole number.
Because the long division is a particular version of the partial quotients method, and because students have been introduced to long division, they have the tools to divide whole numbers that result in a (terminating) decimal. In this activity, students evaluate and critique the reasoning of others (MP3).
Launch
Arrange students in groups of 2. Provide access to graph paper. Give students 7–8 minutes to analyze and discuss Lin’s work with a partner and then complete the second set of questions.
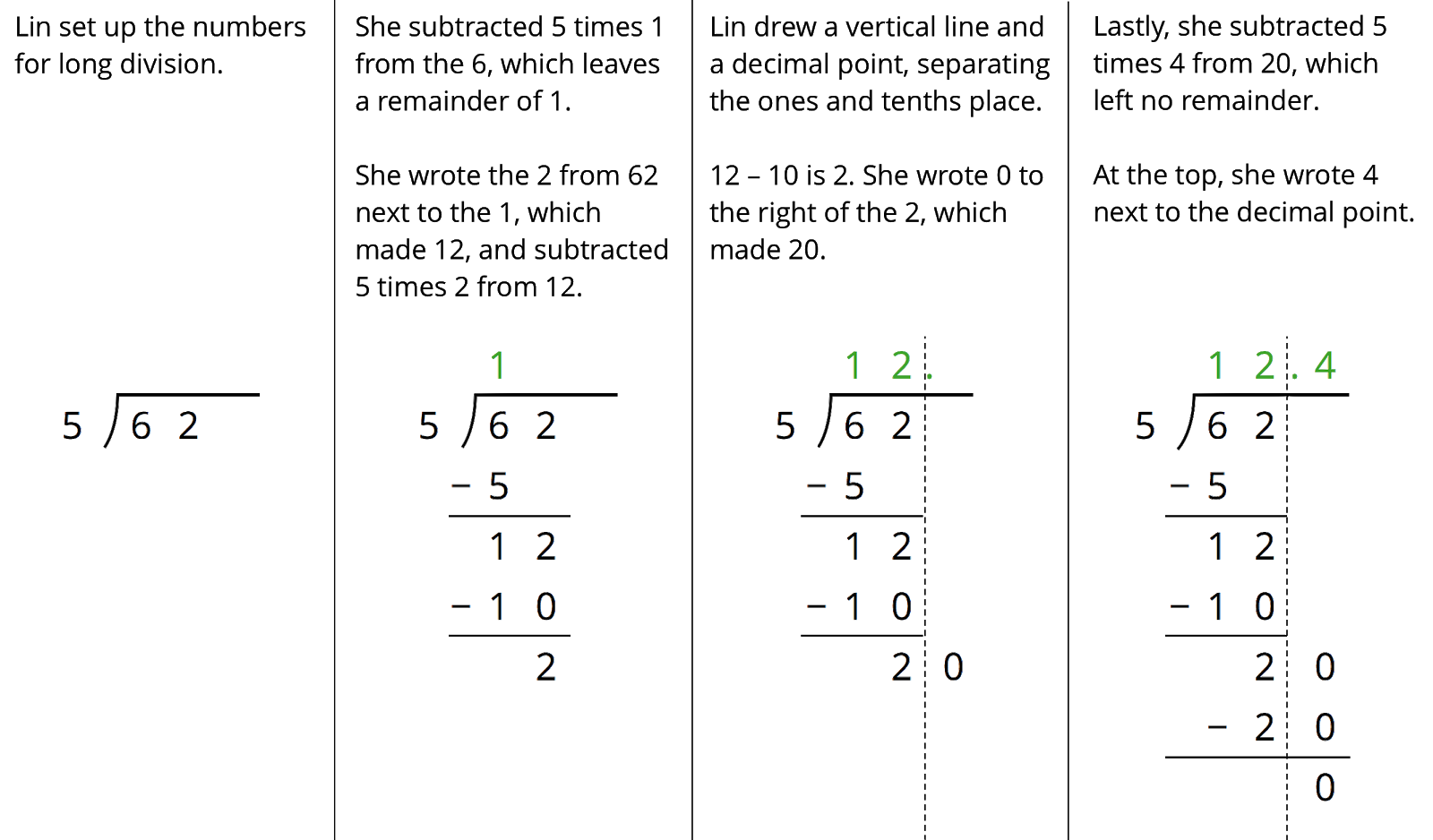
Pause to discuss students’ analyses and at least one of the division problems. Students should understand that, up until reaching the decimal point, long division works the same for 62÷5=12.4 as it does for 657÷3=219. In 62÷5, however, there is a remainder of 2 ones, and we need to convert to the next smaller place value (tenths), change the 2 ones into 20 tenths, and then divide these into 5 equal groups of 4 tenths.
Prepare students to do the last set of questions by setting up the long division of 5÷4 for all to see. Discuss the placement of the decimal point. Reiterate that we can write extra zeros at the end of the dividend, following the decimal point, so that remainders can be worked with. Have students work through this problem and the others. Follow with a whole-class discussion.
Support for Students with Disabilities
Fine Motor Skills: Eliminate Barriers. Provide grid or graph paper for students to organize their work when calculating.
Student Response
- Answers vary. Sample response:
- Lin put a 0 after the 2 because she could not take any more 5’s from 2 but wanted to continue the calculation to the tenths place. The 0 represents 0 tenths and 20 tenths has the same value as 2 ones.
- The 4 in the quotient represents 4 tenths. 20 tenths is 5 equal groups of 4 tenths, and so 4 tenths is added to the quotient.
- The value of 62÷5 is 12.4. There was no remainder after putting 1 ten, 2 ones, and 4 tenths into 5 equal groups.
Opening
Here is how Lin calculated 62 ÷ 5.
Discuss with your partner:
- Lin put a 0 after the remainder of 2. Why? Why does this 0 not change the value of the quotient?
- Lin subtracted 5 groups of 4 from 20. What value does the 4 in the quotient represent?
- What value did Lin find for 62÷5?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will solve real-world problems by dividing whole numbers.
Opening
Solve real-world problems by dividing whole numbers.
Solve Real-World Division Problems
Lesson Guide
Have students work individually. They should choose just one problem to work on. Make sure that there are students working on each of the four problems so that they can all be discussed.
Mathematics
If students are struggling with the division algorithm, you might walk through the solution with them step by step.
Students should check that the answers are reasonable and make sense in the contexts of the problems. Each problem in this task involves the same division, but the answers differ depending on the situation. Students need to consider whether their answer should be a whole number, a mixed number, or a decimal. If the answer is a whole number, do they need to drop the remainder or round to the next whole number? Is the remainder the answer?
Encourage students to check their answers using estimation or multiplication.
Select students to present so that all four problems are represented. Look for students who offer clear explanations and whose reasoning takes into consideration the problem contexts.
Interventions
Student has trouble understanding how the answer should be reported.
- You are dividing an amount of money. Does it make sense to give the answer as a whole number plus a remainder? In what form are money amounts usually given?
- What does the remainder mean in this situation? Can the student council buy a part of a sweatshirt?
- What does the remainder mean in this situation? Where will the “leftover” campers sleep?
- What do the whole number and the remainder represent in this situation? What is the answer to the question that is asked?
Student gets an incorrect solution.
- Can you use estimation to check your answer?
- Go back and read the problem again. Does your answer make sense in the situation?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must consider the problems carefully to determine what they are being asked and to devise a strategy for finding it. The context of the problem determines how the answer should be reported. Students need to consider whether the answer should be a whole number, a decimal, or a mixed number. In the fourth problem, they need to understand why the answer is the remainder.
Mathematical Practice 4: Model with mathematics.
The problems illustrate how we can model real-world problems with mathematical expressions. The Challenge Problem asks students to create their own models for the real world.
Answers
All the problems involve the same mathematical expression, 693 ÷ 12, but they have different answers.
- Each person pays $57.75.
- The student council can buy 57 sweatshirts.
- The summer camp needs 58 cabins.
- The employee gets to keep 9 scones.
Challenge Problem
Answers
- Problems will vary.
Mathematics
Discuss both incorrect and correct solutions. For each problem, prompt students to consider these questions:
- How can you tell whether the answer will be a whole number, a decimal, or a fraction?
- What does the whole number quotient mean in this situation? What does the remainder mean?
For the Camping Trip problem, if a student got the decimal answer by adding a decimal point and a 0 to the dividend and continuing to divide, be sure to discuss that solution method.
If time allows, ask students to present the word problems they wrote for the Challenge Problem. If several students completed the Challenge Problem, you might create a bank of their word problems and ask other students to each choose two problems to solve as part of the Exercises.
ELL: Create an anchor chart with the word problems. As students present their solutions, illustrate on the chart each of the possible ways to represent the solution. If possible, use pictures and make connections between the different solutions. Students should see that there are multiple ways to represent a solution. Display this anchor chart in a prominent location in your classroom as a visual representation of learning that can be referenced in future lessons. Students will use the anchor chart to approach future problems in a more efficient way.
Work Time
Solve Real-World Division Problems
Choose one of the following problems to solve and show your work. Each member within your group of 4 should choose a different problem to solve.
- Twelve friends went on a camping trip. The total cost for the campsite, food, supplies, and gas was $693. If the friends split the cost evenly, how much did each person pay?
- The student council is planning a school sweatshirt sale. The council members found a supplier who charges $12 per sweatshirt, but they have to pay the money up front. If they have $693, how many sweatshirts can they buy?
- Each cabin at a summer camp can hold 12 campers. If 693 students sign up for the camp, how many cabins will be needed?
- An employee at a bakery packaged 693 scones in boxes that each hold 12 scones. Her boss told her that she could keep any extra scones for herself. How many scones did the employee get to keep?
Ask yourself:
- Camping Trip Problem: How can you represent the amount left over in this situation?
- Sweatshirt Problem: Can you buy a fraction of a sweatshirt?
- Cabin Problem: Where will the “leftover” campers sleep?
- Bakery Problem: Will the answer be the number of boxes the employee packed or the number of scones left over?
Challenge Problem
- Write two word problems that you would solve using the same whole-number division expression, but that have different solutions.
Writing Remainders to Match Contexts
Students will use the standard algorithm to solve each problem. They will write the remainder in a context that matches the problem.
Student Responses
1. Sandra will pay $287.50 each month.
2. The district will be able to buy 284 8/10 or 284 4/5 pounds of paper.
3. The hotel will be able to buy 138 pillows.
4. The Mays family traveled 249 11/13 feet each day.
Work Time
Read and solve each problem using the standard algorithm. Write the remainder in a form that matches the context.
1. Sandra buys a new TV for $3,450. She agrees to make equal payments each month for 12 months to pay for it. How much will she pay each month?
2. A school district has $4,272 to spend on pounds of paper. If each pound of paper cost $15 and the school district spent all of their allotted amount of money, how many pounds of paper will the district be able to buy?
3. A hotel has $2,220 to buy new pillows. If the cost of each pillow is $16, how many pillows will the hotel be able to buy?
4. The river route to the Mayan ruins is 3,248 feet long. The Mays family took 13 days to canoe the length of it. If they traveled the same amount each day, how many feet did they travel each day?
Cool - Down: Expressing Remainders
Students Responses
a. Whole Number/No Remainder
b. Fraction
c. Decimal
How would you express the remainder in each of these situations?
a. Put 29 eggs into groups of 4
b. Share 29 licorice sticks among 4
c. Evenly split a $29 pizza deal among 4 friends