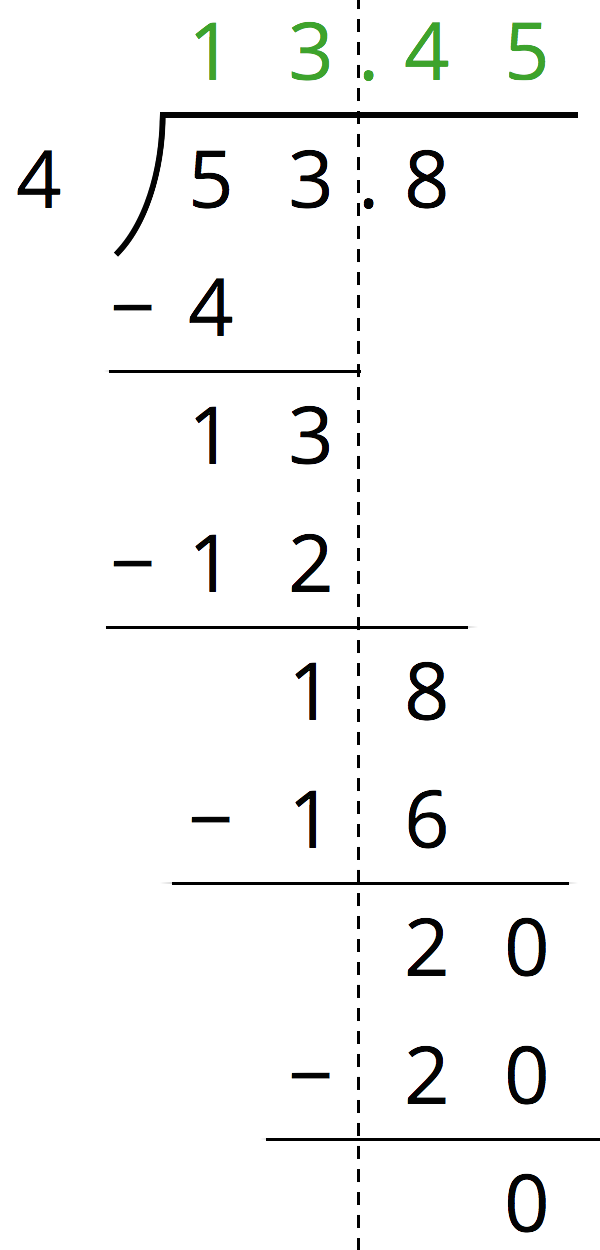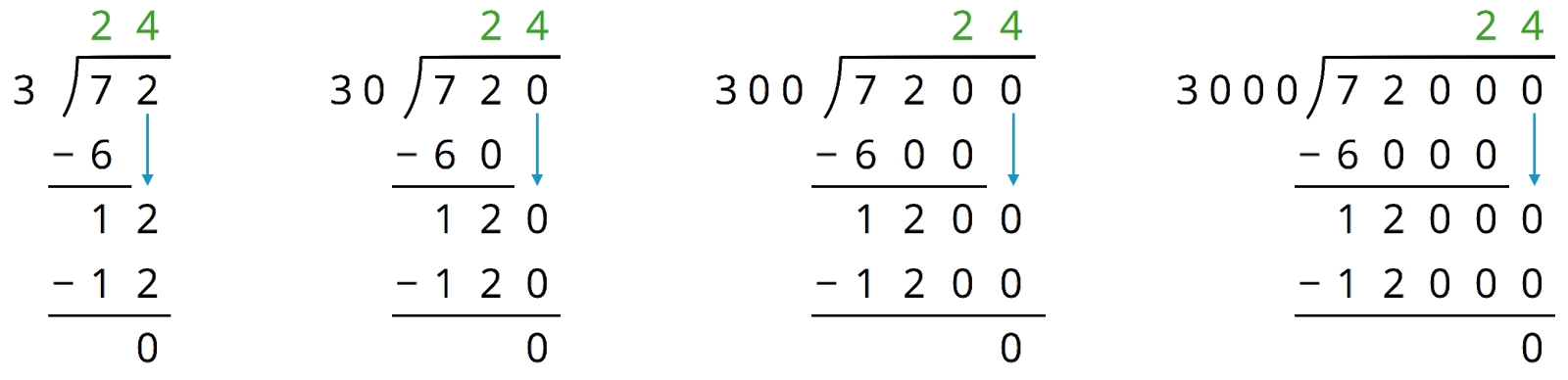6.NS.B.3 Lesson 4

Overview
This lesson serves two purposes. The first is to show that we can divide a decimal by a whole number the same way we divide two whole numbers. Students first represent a decimal dividend with base-ten diagrams. They see that, just like the units representing powers of 10, those for powers of 0.1 can also be divided into groups. They then divide using another method—partial quotients or long division—and notice that the principle of placing base-ten units into equal-size groups is likewise applicable.
The second is to uncover the idea that the value of a quotient does not change if both the divisor and dividend are multiplied by the same factor. Students begin exploring this idea in problems where the factor is a multiple of 10 (e.g. 8÷1=80÷10). This work prepares students to divide two decimals in the next lesson.
Warm Up - Number Talk: Dividing by 4
The purpose of this number talk is to help students use the structure of base-ten numbers and the distributive property to solve a division problem involving decimals.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time for each problem and ask them to give a signal when they have an answer and a strategy. Keep all problems displayed throughout the talk. Follow with a whole-class discussion.
Support for Students with Disabilities
Memory: Processing Time. Provide sticky notes or mini whiteboards to aid students with working memory challenges.
Student Response
- 20
- 3
- 0.3
- 20.3
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone have the same strategy but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
Highlight the use of the distributive property in finding 81.2÷4. Students should recognize that since 81.2=80+1.2, we have 81.2÷4=(80÷4)+(1.2÷4). To make this clear, consider explaining that the division could be equivalently represented by 81.2⋅14=(80+1.2)⋅14=(80⋅14)+(1.2⋅14).
Find each quotient mentally.
80 ÷ 4
12 ÷ 4
1.2 ÷ 4
81.2 ÷ 4
Using Diagrams to Represent Division
Students have learned several effective methods to divide a whole number by a whole number, including cases when there is a remainder. The goal of this task is to introduce a method for dividing a decimal number by a whole number. Students notice that the steps in the division process are the same as when dividing a whole number by a whole number, whether the division is done with base-ten diagrams, as in this task, or using partial quotients or the division algorithm as in future tasks. Here, students need to think even more carefully about place value and where the decimal point goes in the quotient.
Throughout this activity, students rely on their understanding of equivalent expressions to interpret the unbundling in Elena’s process. For example, to unbundle a one into ten tenths means going between the expressions 1 and 0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1.
Launch
Give students 1–2 minutes of quiet think time for students to analyze Elena’s work. Pause and discuss with the whole class. Select a couple of students to share their analyses of what Elena had done to divide a decimal by a whole number.
Support for Students with Disabilities
Conceptual Processing: Manipulatives. Provide manipulatives (i.e., base-ten blocks), to aid students who benefit from learning in concrete contexts.
- another method.
Student Response
-

- 13.45. Each group has 1 ten, 3 ones, 4 tenths, and 5 hundredths.
Opening
To find 53.8 ÷ 4 using diagrams, Elena began by representing 53.8.
She placed 1 ten into each group, unbundled the remaining 1 ten into 10 ones, and went on distributing the units.

This diagram shows Elena’s initial placement of the units and the unbundling of 1 ten.

Complete the diagram by continuing the division process. How would you use the available units to make 4 equal groups?
As the units get placed into groups, show them accordingly and cross out those pieces from the bottom. If you unbundle a unit, draw the resulting pieces.
What value did you find for 53.8 ÷ 4? Be prepared to explain your reasoning.
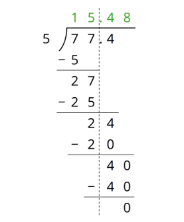
Using Standard Algorithm to Divide Decimal by Whole Number
Students will use long division to find 53.8 ÷ 4 and 77.4 ÷ 5.
Student Responses
- 53.8÷4=13.45 and (13.45)⋅4=53.8
2. 15.48. Sample reasonings:
- There are five groups of 15 in 77 with 2 left over. There are 0.4 groups of 5 in 2.4 with 0.4 remaining. There are 0.08 groups of 5 in 0.40, so 77.4 can be divided into five equal groups of 15.48.
Anticipated Misconceptions
Some students may stop dividing when they reach a remainder rather than unbundling the remainder into smaller units. Remind them that they can continue to divide the remainder by unbundling and to refer to Elena’s worked-out example or those from earlier lessons, if needed.
Work Time
1. Use long division to find 53.8 ÷ 4. Check your answer by multiplying it by the divisor 4.
2. Use long division to find 77.4 ÷ 5. If you get stuck, you can draw diagrams or use another method.
Dividends and Divisors
In this activity, students study some carefully chosen quotients where the dividends are decimal numbers. The key goal here is to notice that there are other quotients of whole numbers that are equivalent to these quotients of decimals. In other words, when the dividend is a terminating decimal number, we can find an equivalent quotient whose dividend is a whole number. In combination with the previous task, this gives students the tools they need to divide a decimal number by a decimal number.
This activity strongly supports MP7. Students notice that, when working with a fraction, multiplying the numerator and denominator in a fraction by 10 does not change the value of the fraction. They use this insight to develop a way to divide decimal numbers in subsequent activities. This work develops students’ understanding of equivalent expressions (6.EE.A.4) by emphasizing that, for example, 8÷1=(8⋅10)÷(1⋅10). Eventually, students will recognize the equivalence of 8÷1 to statements such as (8⋅y)÷(1⋅y). However, in this activity, students only examine situations where the dividend and divisor are multiplied by powers of 10.
Tell students that they’ll analyze the sizes of dividends and divisors more closely to help them reason about quotients of numbers in base ten.
Give students 7–8 minutes of quiet work time to answer the four questions followed by a whole-class discussion.
Support for Students with Disabilities
Receptive/Expressive Language: Peer Tutors. Pair students with their previously identified peer tutors to aid in comprehension and expression of understanding.
Conceptual Processing: Processing Time. Check in with individual students, as needed, to assess for comprehension during each step of the activity.
Student Response
- 10 times
- 10 times
- “equal to” or “the same size as”
- c. 720,000 ÷ 30,000
- 7.2 ÷ 0.3
- B, D, E, and F
Activity Synthesis
Ask students to write a reflection using the following prompt:
What happens to the value of the quotient when both the divisor and the dividend are multiplied by the same power of 10? Use examples to show your thinking.
The goal of this discussion is to make sure students understand that the value of a quotient does not change when both the divisor and the dividend are multiplied by the same power of ten. Ask students to explain why 2520=250200. Possible responses include:
- Both the numerator and denominator of 250200 have a factor of 10, so the fraction can be written as 2520.
- Both fractions are equivalent to 54.
- Dividing 250 by 200 and 25 by 20 both give a value of 1.25.
Tell students that their observations here will help them divide decimals in upcoming activities.
Work Time
Analyze the dividends, divisors, and quotients in the calculations, then answer the questions.
1. Complete each sentence. In the calculations above:
a. Each dividend is ______ times the dividend to the left of it.
b. Each divisor is ______ times the divisor to the left of it.
c. Each quotient is _____________________ the quotient to the left of it.
2. Suppose we are writing a calculation to the right of 72,000÷3,000. Which expression has a quotient of 24? Be prepared to explain your reasoning.
a. 72,000 ÷ 30,000
b. 720,000 ÷ 300,000
c. 720,000 ÷ 30,000
d. 720,000 ÷ 3,000
3. Suppose we are writing a calculation to the left of 72 ÷ 3. Write an expression that would also give a quotient of 24. Be prepared to explain your reasoning.
4. Decide which of the following expressions would have the same value as 250 ÷ 10. Be prepared to share your reasoning.
a. 250 ÷ 0.1 b. 25 ÷ 1 c. 2.5 ÷ 1
d. 2.5 ÷ 0.1 e. 2,500 ÷ 100 f. 0.25 ÷ 0.01
Cool - Down: The Same Quotient
Student Response
- 14.5
- Answers vary. Sample reasonings:
- Each dividend is 20 times the divisor.
- Each dividend is 10 times the dividend below it. Each divisor is 10 times the divisor below it. The quotient of each pair of numbers is therefore the same.
1. Use long division to find the value of 43.5 ÷ 3.
If you get stuck, you can draw base-ten diagrams. Be sure to say what each type of figure represents in your diagrams.
2. Explain why all of these expressions have the same value.
100 ÷ 5 10 ÷ 0.5 1 ÷ 0.05