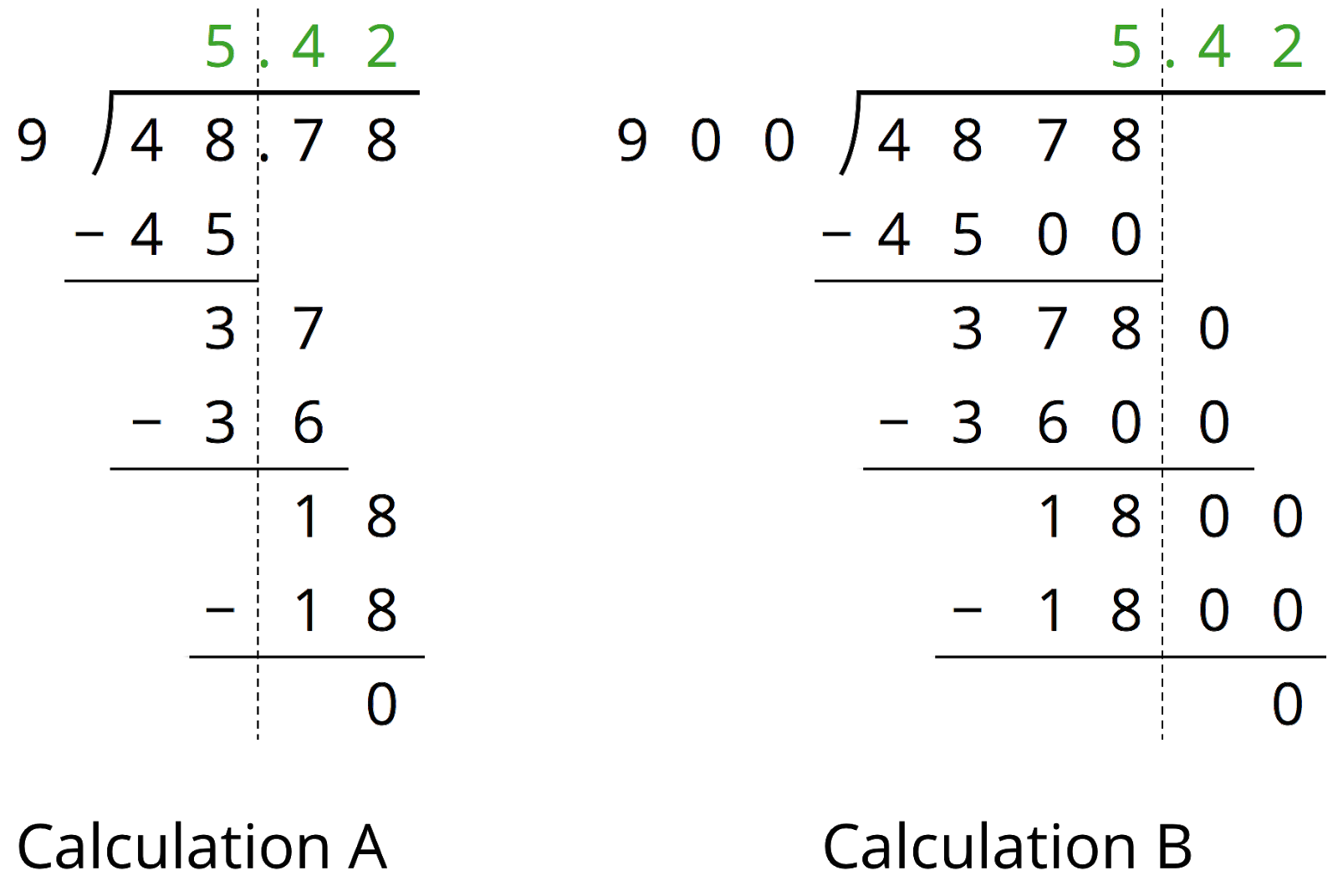6.NS.B.3 Lesson 5

Overview
In the previous lesson, students learned how to divide a decimal by a whole number. They also saw that multiplying both the dividend and the divisor by the same power of 10 does not change the quotient. In this lesson, students integrate these two understandings to find the quotient of two decimals. They see that to divide a number by a decimal, they can simply multiply both the dividend and divisor by a power of 10 so that both numbers are whole numbers. Doing so makes it simpler to use long division, or another method, to find the quotient. Students then practice using this principle to divide decimals in both abstract and contextual situations.
Warm Up - Same Values
In this warm-up, students continue the decimal division work from the previous lesson and do so in the context of money. The work reinforces the idea that the value of a quotient does not change if the numerator and denominator are both multiplied by the same power of 10.
Launch
Give students a moment to read the first question and to estimate whether the quotient will be less than 1 or more than 1. Ask them to give a signal when they have an estimate and can explain it. Ask one student from the “more than 1” group to explain their reasoning and another from the “less than 1” group to do the same. Clarify that the quotient will be less than 1 and give students a few minutes to complete the questions. If time is limited, ask students to work only on the second question. Follow with a whole-class discussion.
Support for Students with Disabilities
Fine Motor Skills: Eliminate Barriers. Provide grid or graph paper for students to organize their work when calculating.
Student Response
- 0.72. Student work should show long division.
- B and D. Sample reasoning:
- Long division can be used to divide 50.4 by 70 and still get 0.72.
- 5.04÷7=50.4÷70 because 5.04 and 7 can be multiplied by 10 to get 50.4 and 70. Multiplying both numbers by the same non-zero factor does not change the quotient.
- 504,000 is 5.04 groups of 100,000, and 700,000 is 7 groups of 100,000. Since the unit of the groups is the same (100,000), examining how many times 7 goes into 5.04, which could simply be represented with 5.04÷7, gives the answer.
Activity Synthesis
Focus the whole-class discussion on the second question. Select several students to explain why choices b and d are correct and why a and c are not. Students should see that 5.04÷70 and 504,000÷700 are not equivalent expressions to 5.04÷7 because the dividend and divisors in each pair are notresults of multiplying the 5.04 and 7 by the same factor or the same power of 10.
1. Use long division to find the value of 5.04 ÷ 7.
2. Which of the following quotients has the same value as 5.04 ÷ 7? Be prepared to explain how you know.
A. 5.04 ÷ 70
B. 50.4 ÷ 70
C. 504,000 ÷ 700
D. 504,000 ÷ 700,000
Two Ways to Calculate Quotients of Decimals
This lesson demonstrates how the division of two equivalent expressions (e.g., 48.78÷9 and 4878÷900) result in the same quotient. By looking at worked-out calculations, students reinforce their understanding about what each part of the calculations represent. The advantage of representing a quotient with a different equivalent expression is so students can simplify problems involving division of decimals by rewriting expressions using whole numbers.
They use the structure of base-ten numbers (MP7) to move the decimal point (through multiplication by an appropriate power of 10). They also use their understanding of equivalent expressions to know that multiplying both the numbers in a division by the same factor does not change the value of the quotient. Both pieces of knowledge allow students to replace a quotient of decimal numbers with a quotient of whole numbers.
Launch
Arrange students in groups of 2. Give partners 5 minutes to discuss the first problem and then quiet work time for the second problem. Follow with a whole-class discussion.
Support for Students with Disabilities
Receptive/Expressive Language: Peer Tutors. Pair students with their previously identified peer tutors to aid in comprehension and expression of understanding.
Student Response
1.
A. Answers vary. Sample response: Both calculations have the same quotient. They both have the same non-zero digits in the dividend and divisor. In Calculation A, the decimal point in the dividend stays. In Calculation B, both the divisor and dividend have been multiplied by 100 so that they are whole numbers. The decimal point in Calculation B is two places to the right of that in Calculation A.
B. The 3 is in the ones place and the 6 is in the tenths place, so 36 means 36 tenths. The 1 in 18 is in the tenths place, so it has the same value as 10 hundredths. The 8 is in the hundredth place. Together, they make 18 hundredths.
C. The 3600 represents 3600 tenths, and the 1800 represents 1800 hundredths.
D. Answers vary. Sample response:
- We can multiply the number of groups and the total amount by 100. 9⋅(5.42)=48.78 and 900⋅(5.42)=4878.
- 900 is 100 times 9. So if 9 groups of 5.42 equal 48.78, then 900 groups of 5.42 equal 100 times 48.78, which is 4,878.
2.
A. 51.2=10⋅(5.12) and 6.4=10⋅(0.64). Multiplying the dividend and the divisor by the same number (10) does not affect the value of the quotient.
B. Answers vary. Sample responses: 512÷64 and 5,120÷640. The long division should show a quotient of 8.
Activity Synthesis
The goal of this discussion is for students to contrast the two division methods used in the task. Discuss:
- Why is the value of 48.78÷9 the same as the value of 4,878÷900? (The numbers in the second expression are both multiplied by 100, and this does not change the value of the quotient.)
- What are some advantages of calculating 48.78÷9 with the decimal intact (the method on the left)? (It is fast, and we don’t need to deal with a bunch of 0’s. Also, if the numbers are from a contextual problem, we could better make meaning of them in their original form.)
- What are some advantages of calculating 4,878÷900 with long division? (These are whole numbers, and we are familiar with how to divide whole numbers. Also, we could express this as a fraction and write an equivalent fraction of 543100, which then tells us that its value is 5.43.)
End the discussion by telling students that they will next look at quotients where both the divisor and the dividend are decimals. The method used here of multiplying both numbers by a power of 10 will apply in that situation as well.
- Here are two calculations of 48.78 ÷ 9. Work with your partner to answer the following questions.
a. How are the two calculations alike? How are they different?
b. Look at Calculation A. Explain how you can tell that the 36 means “36 tenths” and the 18 means “18 hundredths.”
c. Look at Calculation B. What do the 3600 and 1800 mean?
d. We can think of 48.78 ÷ 9 = 5.42 as saying “there are 9 groups of 5.42 in 48.78.” We can think of 4878 ÷ 900 = 5.42 as saying “there are 900 groups of 5.42 in 4878.” How might we show that both statements are true?
2. a. Explain why 51.2 ÷ 6.4 has the same value as 5.12 ÷ 0.64.
b. Write a division expression that has the same value as 51.2 ÷ 6.4 but is easier to use to find the value. Then, find the value using long division.
Practicing Division with Decimals
In this activity, students practice calculating quotients of decimals by using any method they prefer. Then, they extend their practice to calculate the division of decimals in a real-world context. The application of division to solve real-world problems illustrates MP4.
As students work on the first three problems, monitor for groups in which students have different strategies used on the same question.
Launch
Arrange students in groups of 3–5. Give groups 5–7 minutes to work through and discuss the first three questions. Ask them to consult with you if there is a disagreement about a correct answer in their group. (If this happens, let them know which student’s work is correct and have that student explain their thinking so all group members are in agreement.)
After all group members have answered the first three questions and have the same answer, have them complete the last question. Follow with a whole-class discussion.
Support for Students with Disabilities
Conceptual Processing: Manipulatives. Provide manipulatives (i.e., base-ten blocks), to aid students who benefit from learning in concrete contexts.
Fine Motor Skills: Eliminate Barriers. Provide grid or graph paper for students to organize their work when calculating.
Student Response
- 35.5.
- 84. The dividend and divisor in 58.8÷0.7 can each be multiplied by 10 to get 588 and 7. The quotient 58.8÷0.7 has the same value as the quotient 588÷7, which equals 84.
- 234. The dividend and divisor can be multiplied by 10 to get 2,574 and 11. The quotient 257.4÷1.1 has the same value as the quotient 2,574÷11, which equals 234.
- She can make 7 bracelets. 170.1÷24.3 is equivalent to 1,701÷243, which is 7.
Anticipated Misconceptions
Some students might have trouble calculating because their numbers are not aligned so the place-value associations are lost. Suggest that they use graph paper for their calculations. They can place one digit in each box for proper decimal point and place-value alignment.
Activity Synthesis
The purpose of this discussion is to highlight the different strategies used to answer the division questions. Select a previously identified group that used different strategies on one of the first three questions. Ask each student in the group to explain their strategy and why they chose it. For the fourth question, ask students:
- “Could the answer be found by calculating the quotient of this expression: 24.3÷170.1?” (No, because the question is asking how many pieces of string of length 24.3 are in the long string of length 170.1. This is equivalent to asking how many groups of 24.3 are in 170.1 or 170.1÷24.3.)
- “What would the quotient 24.3÷170.1 represent in the context of the problem?” (This quotient would represent what fraction the length of bracelet string is of the full length of string.)
Work Time
Find each quotient using a method of your choice. Then discuss your calculations with your group and agree on the correct answers. If someone in your group makes an error, stop and help that person revise their work. If your group is unsure about an answer, consult your teacher.
A. 106.5 ÷ 3 B. 58.8 ÷ 0.7 C. 257.4 ÷ 1.1
D. Mai is making friendship bracelets. Each bracelet is made from 24.3 cm of string. If she has 170.1 cm of string, how many bracelets can she make? Explain or show your reasoning.
Cool - Down: The Quotient of Two Decimals
Student Response
- Answers vary. Sample responses: 3.68 ÷ 0.23 and 368 ÷ 23.
- 16.
- Write two division expressions that have the same value as 36.8 ÷ 2.3.
- Find the value of 36.8 ÷ 2.3. Show your reasoning.