What Makes a Triangle a Triangle?
Opening
What Makes a Triangle a Triangle?
- What do you know about this figure?
- What makes a triangle a triangle?



Build triangles and explore the angle relationships in triangles.
Start with a sheet of paper. Fold the left edge toward the center at a slant. Unfold. Fold the right edge toward the center so that the fold overlaps the first fold you made. Unfold. Fold the bottom edge toward the center so that the fold overlaps the first two folds you made. Unfold.
Look at the figure that is outlined by the folds.
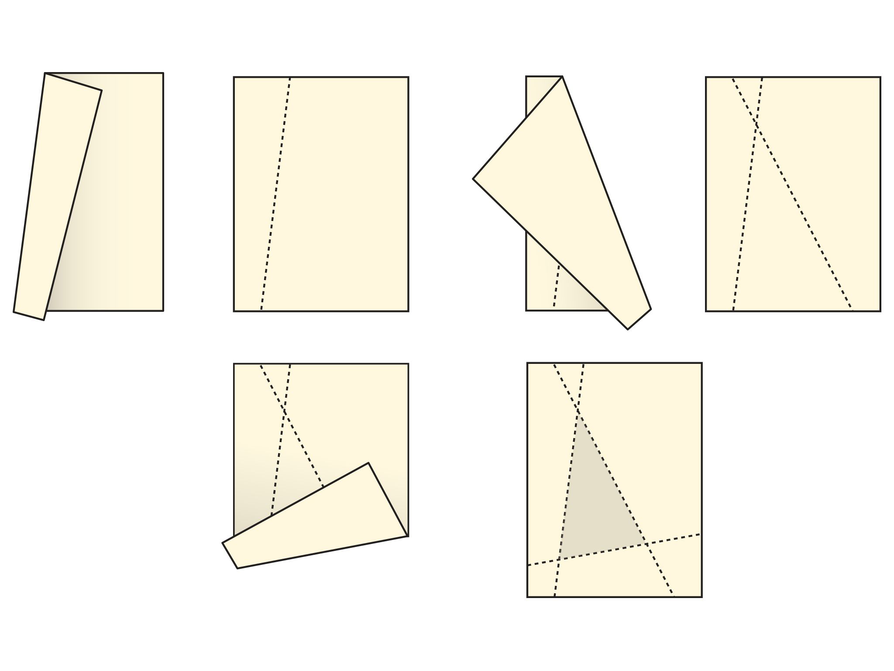
On the same sheet of paper, choose a corner and fold it toward the center. Unfold.
Look at the figure outlined by the edges of the paper and the fold.

On a new sheet of paper, using your protractor and its ruler side, draw triangles with the following characteristics:
Explain how you constructed different types of triangles. Use your work to support your explanation.
Take notes about your classmates' conclusions and explanations for their triangles.
As your classmates' present, ask questions such as:
Write a summary about the angles in a triangle.
Check your summary:
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I think a triangle is similar to a quadrilateral because ...