Tessellations
Work Time
Tessellations
Part I
If the angles that form a complete circle around a vertex are the interior angles of regular polygons, then those polygons can form the basis of a repeating pattern called a tessellation.
The first two images use regular polygons. This pattern is called a regular tessellation.
- A regular tessellation is made using six regular polygons around each point.
- What is the measure of an interior angle of that regular polygon?
- How many sides does that regular polygon have?
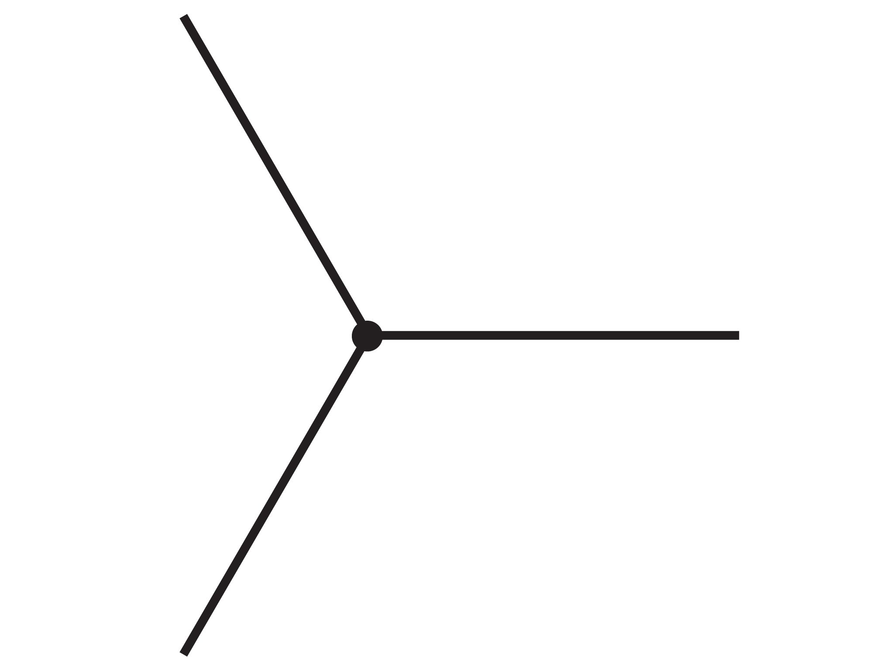
- A regular tessellation is made using three regular polygons around each point.
- What is the measure of an interior angle of that regular polygon?
- How many sides does that regular polygon have?

Part 2
The second pattern is called a semi-regular tessellation, because it uses more than one type of regular polygon.
- A semi-regular tessellation is made using four regular polygons around each point.
- What is the measure of an interior angle for each regular polygon?
- How many sides does each regular polygon have?
- It is possible to arrange two regular octagons and one square around one point.
- Explain why.
- Sketch a part of the semi-regular tessellation that is produced by this arrangement.
- Work with your partner to create a list of as many regular and semi-regular tessellations as you can.
