- Author:
- Vicky Hindle
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- High School
- Grade:
- 12
- Tags:
- License:
- Creative Commons Attribution Non-Commercial Share Alike
- Language:
- English
- Media Formats:
- Text/HTML
Calculating sample standard deviation
Overview
By the end of this session, you will be able to:
- Define standard deviation
- Calculuate starndard deviation
- Interpret standard deviation scores
What is standard deviation:
What is standard deviation?
Standard deviation is a measure of dispersion. To understand what standard deviation is, we need to look at what the two words mean.
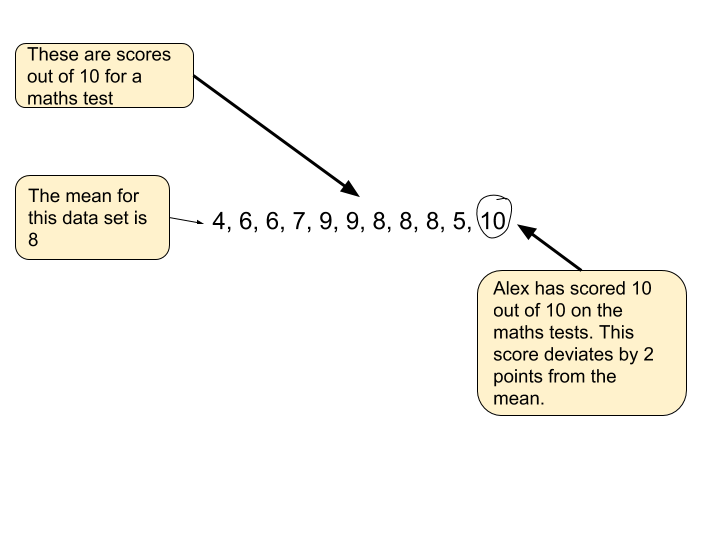
Deviation: The term deviation means, ‘departure from the standard or norm.’ (Dictionary.com, 2018, p1). In statistics, it refers to how much an individual’s score differs from an average score in a distribution as the image below illustrates . As you can see, the average score for this maths test is 8. Alex has scored 10 points, so deviates by 2 points from the average.
Standard: Standard means ‘typical or average’ (Urdan, 2016, p.22).
Therefore, standard deviation indicates how far individual scores within a data set are from the mean (Urdan, 2016)
Steps for calculating the standard deviation
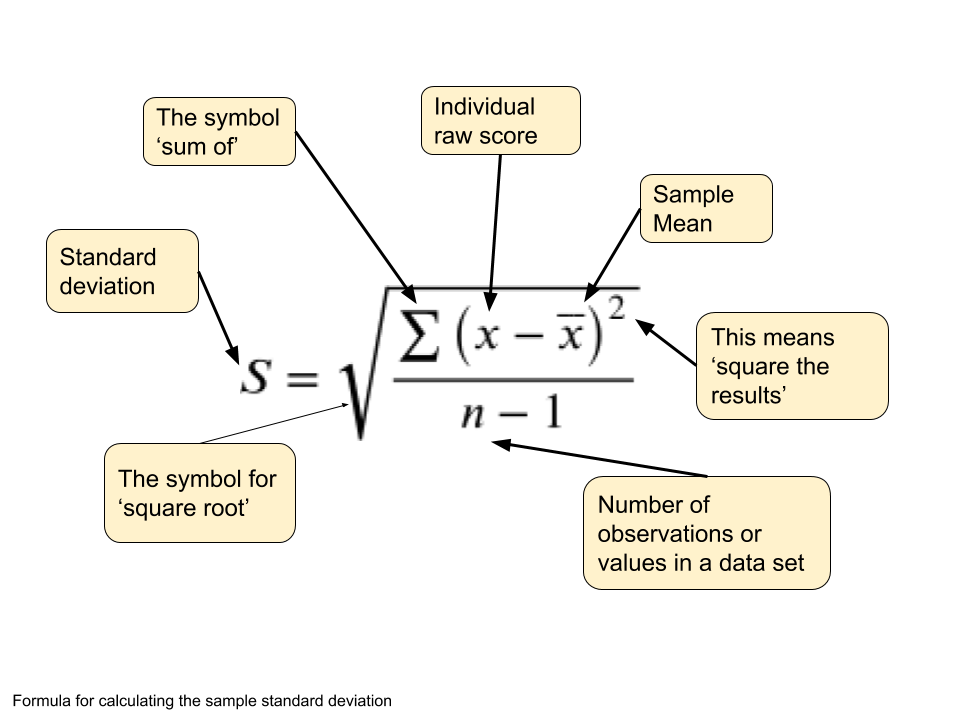
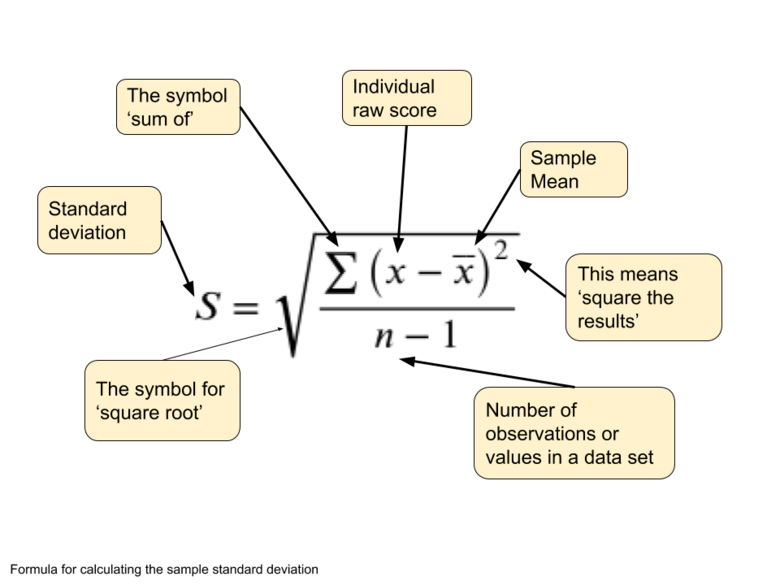
This is the formula for calculating the standard deviation:
Don’t be put off by the formula. This formula just gives you the steps you need to calculate the standard deviation. These steps are explained
Scenario: A researcher has recorded the time it takes for participants to solve a puzzle without any distraction. These are the results: 23, 19, 24, 47, 23, 20
The steps, below, show how to calculate the standard deviation for a sample
Interpreting standard deviation scores
We have just worked out that the standard deviation for group A is 10.47. However, what does this mean?
10.47 is a large standard deviation (SD). The larger the SD the ‘more spread out the data is’ from the mean. In other words, some of individual numbers in a data set deviates far from the average. For example, the mean for group A is 26. However, one of the individual scores is 47 so is quite far from this average.
On the other hand, a low SD indicates that most of the numbers in your data set are close to the average. For example, a score of 24 is close to the average of 26.
References:
DataStar (ND) How to Interpret Standard Deviation and Standard Error in Survey Research http://www.surveystar.com/startips/std_dev.pdf (Accessed 1st of November 2018)
Urdan, T.C. (2017) Statistics in Plain English, Oxon: Routledge
Activity:
Work out the standard deviation for this data set to 2 decimal places:
44, 43, 44, 46, 48
What does this standard deviation tell us about this data set?
If you get stuck, watch the video below.
Answer
1.79 to 2 decimal places