Description
- Overview:
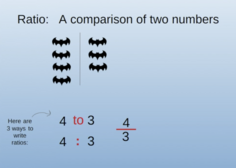
- This lesson teaches about Rates, Ratios, and Unit Rates, using visually appealing art and real-life examples that will engage teenagers.
- Subject:
- Ratios and Proportions
- Level:
- Upper Primary, Middle School, High School
- Material Type:
- Lesson
- Author:
- Janel Williams
- Date Added:
- 01/15/2021
- License:
-
Creative Commons Attribution

- Language:
- English
- Media Format:
- Text/HTML
Comments
Standards
Learning Domain: Ratios and Proportional Relationships
Standard: Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Use ratio and rate reasoning to solve real-world and mathematical problems.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Solve unit rate problems including those involving unit pricing and constant speed.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Compute unit rates, including those involving complex fractions, with like or different units.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Recognize and represent proportional relationships between quantities.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, "The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak."ť "For every vote candidate A received, candidate C received nearly three votes."ť
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ‰äĘ 0 (b not equal to zero), and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar." "We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger." (Expectations for unit rates in this grade are limited to non-complex fractions.)
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Solve unit rate problems including those involving unit pricing and constant speed. For example, If it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured in like or different units. For example, if a person walks 1/2 mile in each 1/4 hour, compute the unit rate as the complex fraction (1/2)/(1/4) miles per hour, equivalently 2 miles per hour.
Degree of Alignment: Not Rated (0 users)
Learning Domain: Ratios and Proportional Relationships
Standard: Recognize and represent proportional relationships between quantities.
Degree of Alignment: Not Rated (0 users)
Cluster: Understand ratio concepts and use ratio reasoning to solve problems
Standard: Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, “The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak.” “For every vote candidate A received, candidate C received nearly three votes.”
Degree of Alignment: Not Rated (0 users)
Cluster: Understand ratio concepts and use ratio reasoning to solve problems
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0 (b not equal to zero), and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar." "We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger." (Expectations for unit rates in this grade are limited to non-complex fractions.)
Degree of Alignment: Not Rated (0 users)
Cluster: Understand ratio concepts and use ratio reasoning to solve problems
Standard: Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
Degree of Alignment: Not Rated (0 users)
Cluster: Understand ratio concepts and use ratio reasoning to solve problems
Standard: Solve unit rate problems including those involving unit pricing and constant speed. For example, If it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?
Degree of Alignment: Not Rated (0 users)
Cluster: Analyze proportional relationships and use them to solve real-world and mathematical problems
Standard: Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured in like or different units. For example, if a person walks 1/2 mile in each 1/4 hour, compute the unit rate as the complex fraction (1/2)/(1/4) miles per hour, equivalently 2 miles per hour.
Degree of Alignment: Not Rated (0 users)
Cluster: Analyze proportional relationships and use them to solve real-world and mathematical problems
Standard: Recognize and represent proportional relationships between quantities.
Degree of Alignment: Not Rated (0 users)
Evaluations
Achieve OER
Average Score (3 Points Possible)| Degree of Alignment | N/A |
| Quality of Explanation of the Subject Matter | 2 (1 user) |
| Utility of Materials Designed to Support Teaching | 3 (1 user) |
| Quality of Assessments | N/A |
| Quality of Technological Interactivity | N/A |
| Quality of Instructional and Practice Exercises | N/A |
| Opportunities for Deeper Learning | 3 (1 user) |

on Nov 07, 06:19pm Evaluation
Quality of Explanation of the Subject Matter: Strong (2)
The video went into details explaining the differences and connections between ratios, rates and unit rate. I love that it explain the multiple ways ratio can be written and that unit rate has a denominator of one. However, the explanation on the LCM can be confusing. I also think it is important to explain the ordering when teaching ratio.
on Nov 07, 06:19pm Evaluation
Utility of Materials Designed to Support Teaching: Superior (3)
Most of the material is easy to understand and its easy to use.
on Nov 07, 06:19pm Evaluation
Opportunities for Deeper Learning: Superior (3)
The material allows for deeper learning because it involves real life examples that students can connect with.