Compare Mia’s Methods
Opening
Compare Mia’s Methods
Emma runs on a -mile track to train for a marathon. Yesterday Emma ran a total of 3 miles. How many times did she run around the track?
Mia decides to solve this problem using a model similar to the one she used to find in the previous lesson.
She reasons:
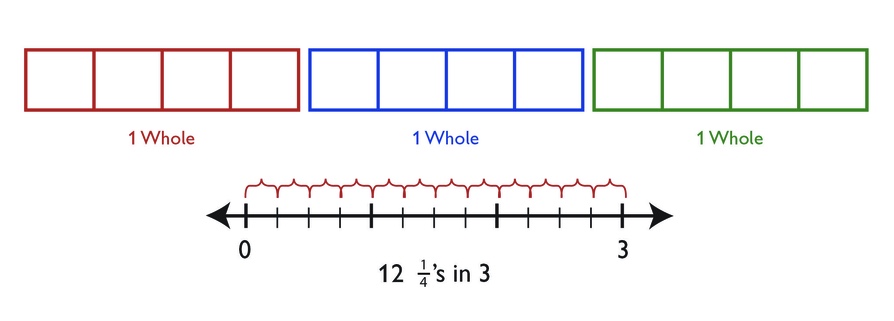
“I need to find the number of miles in 3 miles. So, I need to find 3 ÷ .
“To make a model of this situation, I can draw a bar for each whole mile and then divide each bar into fourths.
“There are 12 fourths in all, so 3 ÷ = 12. Emma ran around the track 12 times.”
- Discuss Mia’s solution. How is her approach similar to the one she used to find ? How is it different?