High quality mathematics resources for remote high school learning from the CK-12 Foundation, EngageNY, Illustrative Mathematics, and Khan Academy. You can refine the collections by selecting different fields, such as material types, on the left side of the page, under Filter Resources.
Overview of the Intermediate Value Theorem, the Extreme Value Theorem and the Mean Value Theorem.
In this task students prove that linear functions grow by equal differences over equal intervals, and that exponential functions grow by equal factors over equal intervals.
This problem illustrates how an exponentially increasing quantity eventually surpasses a linearly increasing quantity.
In this task students observe using graphs and tables that a quantity increasing exponentially eventually exceeds a quantity increasing linearly, quadratically, or (more generally) as a polynomial function.
This problem shows that an exponential function takes larger values than a cubic polynomial function provided the input is sufficiently large.
The purpose of this task is to help students see the "why" behind properties of logs that are familiar but often just memorized (and quickly forgotten or misremembered). The task focuses on the verbal definition of the log, helping students to concentrate on understanding that a logarithm is an exponent, as opposed to completing a more computational approach.
This task and its companion, F-BF Exponentials and Logarithms I, is designed to help students gain facility with properties of exponential and logarithm functions resulting from the fact that they are inverses.
This 8-minute video lesson looks at adding and subtracting rational expressions.
This 4-minute video lesson looks at multiplying and dividing rational expressions.
This 5-minute video lesson looks at multiplying and dividing rational expressions.
This 4-minute video lesson looks at multiplying and dividing rational expressions.
The goal of this task is to develop an understanding of why rational exponents are defined as they are (N-RN.1), however it also raises important issues about distinguishing between linear and exponential behavior (F-LE.1c) and it requires students to create an equation to model a context (A-CED.2
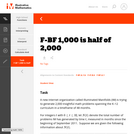
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
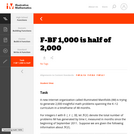
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The table below shows some input-output pairs of two functions $f$ and $g$ that agree for the values that are given but some of their output values are...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Standard maps of the earth are broken into a grid of latitude lines (east-west) and longitude lines (north-south). Consider the function, $N(\ell)$, th...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: A model airplane pilot is practicing flying her airplane in a big loop for an upcoming competition. At time $t=0$ her airplane is at the bottom of the ...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: You are a marine biologist working for the Environmental Protection Agency (EPA). You are concerned that the rare coral mathemafish population is being...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The table below shows historical estimates for the population of London. Year18011821 18411861 18811901 1921 1939 1961 London population 1,100,000 1,60...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Pictured below are the graphs of four different functions, defined in terms of eight constants: $a, b, c, k, m, p, q, \text{ and } r.$ The equations of...