Integers lesson 1.2

Created Feb. 7, 2024 by Susan Jones

Unit one can be found at https://www.oercommons.org/authoring/13198-integers-introduction-to-the-concept-with-activiti/view   

Part 1: Lesson Description

Lesson Title

1.2   Integers:   Application of number line concepts to number lines

Links to Other Documents & Materials (student text, student practice)

This lesson pertains to “Section 1.2:  The Number Line”

Download: Chapter one transitions integers_1.docx  

as Open Document Format (draft)  

Download: Chapter One Transitions Math April2016.odt

Google Doc link: Chapter One Transitions Math Google Doc

Key with Teacher's Notes and Comments:   

Download: Chapter One Transitions Integers Key.docx

Google Docs Link:   Chapter One Transitions Math (Integers) Answer Key - Google Doc

Geogebra activity placing integers between -15 and 15 on number line: 

    Vertical https://www.geogebra.org/m/zFHK5sqS  

    Horizontal https://www.geogebra.org/m/T9jPesSF

 https://www.youtube.com/watch?v=92Jv33rzpjI    Intro to number lines -- just positive numbers.  

https://www.youtube.com/watch?v=x0E4vxLydNY   -- video from Public Broadcasting Service with teens explaining "positive" and "negative" in terms of YouTube Thumbs Up and Thumbs Down, and borrowing money.   

Blog with links to printable math posters --https://mathequalslove.blogspot.com/p/free-classroom-posters.html  

 https://app.box.com/s/dlesfh0x02oln2r32qy4  -- dropbox with printable number lines

 Abstract

For many adult students, positive and negative integers are an example of when math “keeps changing the rules.”  Thisis the secondof six lessons guiding students in constructing the abstract concepts necessary to understand adding positive and negative integers.  

    This lesson will review the newly introduced concept of negative numbers as below zero on a thermometer, with practice labeling thermometers and using the different terms (e.g., less than, negative, positive) in different contexts.  This more-likely-to-be-familiar concept (especially here in Illinois where temperatures do go below zero) will be extended to the number line.   

Learner Audience / Primary Users

This lesson is part of a structured sequence of multisensory, conceptual lessons building basic math concepts for students who struggle with number sense and arithmetic, especially figuring out what to do with practical problems.   It is taken from Parkland College's "Transitions" course for students whose placement test scores do not qualify them for Pre-algebra.   In 4 semesters, fewer that 5% of students have questioned whether their placement was valid.   They recognize the need for more than a quick review of math.  

  Educational Use

  • Curriculum / Instruction
  • Professional Development College & Career Readiness Standards (CCRS) Alignment
  • Level: Adult Education
  • Grade Level:
  • Subject: Mathematics
  • Domain or Strand:  
  • Number Sense
  • Primarily Math Practices 1, 2  
  • Level D   (because it includes negative numbers --   It is not assumed that students are competent with the first three levels.)
  • Standard Description: Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates. (6.NS.6) • Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., –(–3) = 3, and that 0 is its own opposite. (6.NS.6a)  
  • Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane. (6.NS.6c) Understand ordering and absolute value of rational numbers. (6.NS.7)
  • Interpret statements of inequality as statements about the relative position of two numbers on a   number line diagram. For example, interpret –3 > –7 as a statement that –3 is located to the right of –7 on a number line oriented from left to right. (6.NS.7a)
  • Write, interpret, and explain statements of order for rational numbers in real-world contexts. For example, write –3º C > –7º C to express the fact that –3º C is warmer than –7º C. (6.NS.7b)

Language

English

Material Type

  • Instructional material
  • Student Text
  • Student practice
  • Lecture Notes
  • Video

Learning Goals

The purpose of this lesson is for learners to be able to:

  • Order a set of integers from least to greatest.
  • Order a set of integers from greatest to least.
  • Recognize that Integers get smaller in value as you move to the left, and larger as you move to the right on a number line.
  • Recognize whether quantities *without numbers* are greater or less than each other based on their positions on the number lines.
  • Apply procedures for comparing and ordering integers to complete  interactive exercises

Keywords

  • Designers for Learning
  • Adult Education
  • Integers
  • Math
  • Math Anxiety
  • Multisensory
  • Learning Disabilities
  • Developmental Math
  • CCRS
  • RI.6.2

Time Required for Lesson

20-30 minutes

Prior Knowledge

Learners should have counting skills and have completed lesson 1.1    This course is designed for students with minimal "prior knowledge" or math skills.

Required Resources

Text and paper and pencil.There are support videos that can be viewed online or downloaded for viewing with a device that can show MP4 videos (computer, tablet, telephone).  

  • Lesson Author: Susan Jones using text  by Kathy Wahl

 

download image

 

Part 2: Lesson

Learning Objectives

By the end of this lesson, the ESL, ABE or GED  learner should be able to:

  • Order a set of integers from least to greatest.
  • Order a set of integers from greatest to least.
  • Recognize that Integers get smaller in value as you move to the left, and larger as you move to the right on a number line.
  • Recognize whether quantities *without numbers* are greater or less than each other based on their positions on the number lines.
  • Apply procedures for comparing and ordering integers to complete  interactive exercises  

Lesson Topics

Key topics covered in this lesson include:

  • Comparing integers on a number line
  • Measuring and comparing cold temperatures and transferring that knowledge to the more abstract number line.  
  • Comparing relationship (greater or less than) based on position on the number line.

Context Summary

     This lesson is the initial entry into math for students whose math background is below what’s expected for adults.  They may have been in special education settings in K-12.  In our setting, they will have taken the Accuplacer math placement test and scored below the required score to place into “Pre-Algebra.”   However, they need more than “test preparation’ and review.  

    These students are usually degree- or certificate- seeking students who  have significant gaps in their arithmetic and algebra skills.  

Relevance to Practice

    Understanding negative numbers is relevant because of their use in topics such as budgeting and science, as well as in required courses and placement tests.  We have moved this chapter to the beginning of the course because we feel it will have the affective advantage of being an abstract, non-elementary math topic, while allowing the teacher to discern the students’ number sense with single-digit operations.   Many students with this placement are still adding by “counting up” or even counting from zero, and we can address this here without the student having to do primary-level math.   For example, students label number lines with positive and negative numbers “counting by fives,” or twos, or tens.    

Key Terms and Concepts

Note:   many of these terms will be “familiar” to learners, but we will be using and applying them in less familiar ways.

Addition

Integer

Negative

Opposite

Parentheses

Positive

Subtraction

Instructional Strategies and Activities

Warm-Up/ (2 minutes but may take longer)

  •  With a number line available for reference  (This sitehas links to several options -  http://mathequalslove.blogspot.com/2014/09/printable-vertical-number-line-foldable.html  has one that can be printed on legal size paper and folded for student notebooks) , tell students that we’re going to get to know these number lines today.   Ask about what positive and negative numbers are, using temperature and money as references (don’t jump to “just number lines and symbols” too quickly!).Ask students how they can explain why -10 is less than -5 even though 10 is more than 5 using those references – or another if they can think of it (elevation or distance to a goal would be possibilities).   
  • If tutoring / working 1:1 with a student, note whether the student naturally looks at the thermometer or number line… or prefers to think about the “Stories” about temperature or money.  Helping the student start  with what comes most naturally and then forging a connection to the other (whether visual or verbal) can help the student take control of learning. 

 

Introduction (4 minutes)

Ask students what they notice about the number line.   What do they wonder about them? 

 Write down student observations so they can see them.   What is usually true?  What is sometimes true?  What *has* to be true for a number line to work/   (For more information about starting lessons with “noticing” and “wondering”, see http://mathforum.org/pow/noticewonder/ )

 

Get to these points:  

    Number lines are based on zero – but you can actually start anywhere.  Arrows at both ends means it could keep going forever. 

     The spaces have to be consistent – but they can be large or small. 

     We traditionally start small on the left and get bigger to the right.

      The “origin” is zero – but now that we’re higher level thinkers, we can go  forward or backward. 

 

 

Presentation / Modeling / Demonstration

Time: 6 minutes

Use text page six – note that we’re going to be switching to a horizontal number line.   However, students may benefit from a vertical number line – see http://mathequalslove.blogspot.com/2014/09/printable-vertical-number-line-foldable.html   for a blog post about using these in “interactive notebooks” and the file to print them out yourself (the files are at https://app.box.com/s/dlesfh0x02oln2r32qy4  ).  

 

Based on the earlier discussion, have students fill in the blanks showing that numbers on the right represent larger amounts than numbers on the left.

 

Then note that we don’t have to know what the numbers even are to figure this out:   a will be greater than b.   B will be smaller than or less than a.  

 

Review the “greater than” and “less than” symbols with students. Some may be helped with these images:

Greater than, equals and less than symbols with pictures of small, medium and big dog to show which is used when.
Greater than, equals and less than symbols with pictures of small, medium and big dog to show which is used when.

Greater than, equals and less than symbols with pictures of small, medium and big dog to show which is used when.

 

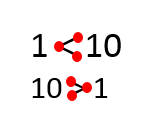
Less than and greater than example images

Less than and greater than example images

Less than and greater than example images

and the idea that the side with more dots is the side with the bigger number; others will enjoy the “alligator” movie linked in the text.

 

Guided Practice

Time: 15 minutes

Complete page 7-8  in student text.

 Encourage students to work together and help each other.

Tell them that Example five is a special challenge – sort of a “trick question.”   If there were no signs on the number *and* number lines went from big to small, it “would be easy.”  

The  goal is that when a student sees "-15", s/he recognizes its negative value and that it is less than -10.   

 

Evaluation

Time: 10-15 minutes (will vary)  

Complete evaluation exercise    The last two exercises are challenging extensions and could also be done in groups.      

Part 3: Supplementary Resources & References

Supplementary Resources

http://www.mathsisfun.com/number-line.html   explanation of positive and negative on number line.  

http://www.mathsisfun.com/positive-negative-integers.html   -- summary of adding

http://www.scholastic.com/teachers/top-teaching/2012/09/positive-approach-teaching-negative-numbers   ideas for teachers for explaining negative numbers  

https://www.youtube.com/watch?v=92Jv33rzpjI   introduction to number line – doesn’t discuss negative numbers.

 

References/Attribution Statements

[Brainzy Games by Education.com] (2014, July 16), Number Gators (Greater Than, Less Than Symbols Song) [Video File] Retrieved from https://www.youtube.com/watch?v=M6Efzu2sla

Transitions, Chapter One contributed by Kathy Wahl and Sue Jones of Parkland College  

This course content is offered   under a CC Attribution license.

Content in this course can be considered under this license unless otherwise noted.      


Return to top