Push and Support Cards: A Bridge to Advanced Mathematics for the Multi-Level Adult Education Classroom Curriculum Guide
This OER curriculum guide is a free resource that supports the integration of OER into teaching plans. It was made possible by funding provided by the U.S. Department of Education Office of Career, Technical and Adult Education (OCTAE) under the project titled: Power in Numbers: Advancing Math for Adult Learners, (OER Math project), managed by Luminary Labs. The opinions expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education and no official endorsement by the U.S. Department of Education should be inferred.
Problem Solving In the Adult Education Classroom

Problem Solving with Push and Support
After analyzing the data collected from PIAAC, The Program for the International Assessment of Adult Competencies, Donna Curry concludes: Addressing adult learners’ attitudes about math to help them build a productive disposition is possibly the greatest challenge for teachers. [1] Many of us who have taught, or who are currently teaching adults, recognize the truth in this statement. Adults many times enter our classes with a belief that they are not a “math person” and that the only way to succeed in math is to memorize procedures. Even adults who enter our classes having experienced some success in math classes in the past, almost always have at least some of those procedures bolloxed up in their memories and have minimal ability to be able to make application of procedures in messy real-world settings that require more than just surface knowledge of one procedure. In both cases, students need to develop conceptual understanding of the math behind the numbers and the symbols, and the ability to think through mathematical situations. In other words, they need to develop problem solving skills.
Students may have wide-ranging ideas on what problem solving means. This isn’t a bad thing. It is valuable to draw out the thinking of our students in terms of what they are already inclined to do when faced with solving a math problem and what they intuitively know about a situation that requires mathematical thinking. Many of our adult students have gotten by in life by using unconventional means to solve math and these creative, out-of-the-box, problem solving methods are where our students are currently at, so we need to meet them there. Sometimes, we can use what they are already doing and help them to build on the foundation they have. At other times, we discover deep rooted misconceptions that need to be adjusted. Either way, our goal is to help our students to make sense of problems and persevere in solving them, MP1. [2] Our goal is not to “show” them how to solve a problem. This will not help them to pass high-stakes exams, nor will it enable them to function as numerate adults.
Collaborative Learning
Push and support cards act as a catalyst for students in their journey to construct viable arguments and critique the reasoning of others, MP3. [2] As already mentioned, our adult students usually come to our classes with some ideas (or sometimes no idea) about how to solve math problems. Creating an environment where they feel safe sharing their angst, their ideas, and their atypical problem solving strategies is vital if they are to become mathematically proficient. There are numerous ways to approach the solving of math problems and this should be encouraged and celebrated. Some of these methods may come out naturally for students as they work together, but if not, the support cards provide recommendations for ways to get started. Suggestions on the cards include, but are not limited to: drawing a picture, using manipulatives, or using a table to organize information.
As they make these connections they develop number sense and confidence that carries forward when they are faced with new and different problems to solve, because they have their knowledge of their own discoveries in problem solving and also awareness of the methods they have seen other students use and talk about. Another important aspect that comes of collaboration is that students can make sense of a math problem by talking through it. When working individually, a student may skip over or misunderstand relevant information, but when students talk about it together, they help each other to make sense of the problem.
Before Using Push and Support in Your Classroom
One first step in understanding how your students might feel when pressed with solving a problem is to spend time solving it yourself. When doing this, if you find that you get stuck, rather than reach for the answer key that is available in the Google doc version of this curriculum guide, you might want to take a look at the push and support cards that correlate with the problem, one at a time, until you’ve come to a solution [3] . Even if you didn’t need the support cards to solve the initial phase of the problem, think about how the support cards might be used by students to help them gain conceptual understanding. For example, some of the cards may suggest that a student draw a picture of the situation or use manipulatives to solve it. I recommend you do the same. This may be a challenge for some instructors who are very familiar with using procedures to solve math problems. What would a picture look like that models the situation? How do you anticipate that students will use the manipulatives to model the math? After this, work through the problems on the push cards; each time anticipating how students will respond to the cards.
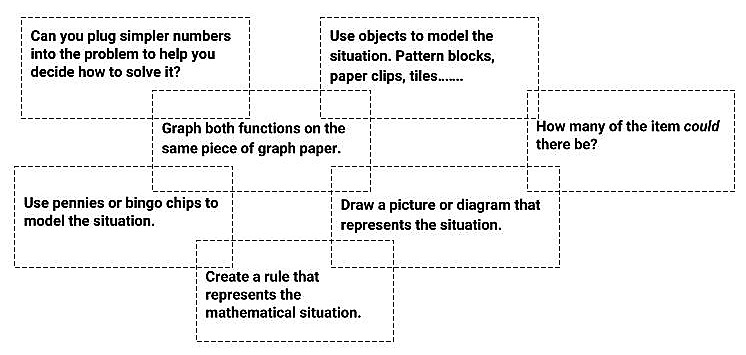
Examples of Push and Support Cards
How to Use Push and Support in Your Classroom
Have in mind before each task how you want to scaffold the cards, moving from support to push. However, keep in mind that some cards can act as a support card or a push card depending on the student (or group). For example, it may be helpful for some students to use manipulatives or draw a picture in order to understand the mathematical situation. On the other hand, other students may understand how to manipulate numbers on paper, but be challenged when asked to draw a picture of the situation. Listed below are some simple steps to take when using the push and support cards
- Allow students 3 - 5 minutes of quiet time to work individually on the initial phase of the task without giving out any cards. This quiet time is essential for some students in order for them to be able to develop their own ideas about a mathematical task. If not given the time, they may shut down in their thinking as soon as a fellow student voices an idea or problem solving strategy. You should be on the lookout for what students are writing during this quiet time and encourage them to share out during group work.
- After quiet time, pair students or have them work in groups of three. Listen to what they are talking about and look at what they are writing on their paper. If they are stuck give the group one support card to share. When possible, try to hand out a card that connects to the solution pathway that they are already moving towards. Make sure that the group understands the information on the card, providing clarifying information if needed, but stop short of explaining the guidance the card is providing. [3]
- Only hand out one card at a time. When the group has exhausted the sharing of their own ideas and strategies and needs more support or suggestions to move forward, give them another card to share. Meantime, if a group has finished working through the suggestion on the card and is ready to take the problem to the next level, provide them with a push card to extend their understanding to more advanced mathematics.
- It is very important to keep in mind that the reason you are using push and support cards is to create a classroom environment where all students can work on the same problem, at the same time, but not necessarily all reach the same level of understanding. Some students may spend the entire time allotted for the activity working with one or two support cards, while other students may work through every push card that you have!
Note: A detailed description of how to use push and support cards is included in the write up of The Painted Cube: one of the Math Memos problems. Download and print: How to Use Push and Support in Your Classroom
Course Description
For the purposes of this curriculum guide, we will think about math problems as a situation in the real-world that involves quantities and context that students would be familiar with or a visual model that can be used by students as a bridge to gain conceptual understanding of abstract mathematical concepts.
These tasks are sometimes referred to as low-floor/high-ceiling tasks because while all students can find a way into the task (low-floor), some students will be able to extend their understanding to the more abstract level (high-ceiling). Low-Floor/High-Ceiling tasks have the following characteristics:
- They have multiple starting points.
- They do not have a readily apparent solution.
- They can be solved using different methods.
- They stimulate discussion.
- They promote productive struggle.
- They require students to make decisions.
These tasks, along with notice/wonder and the push and support cards, can be used with a group of heterogeneous students, but the problems contained or linked to in this guide also work very well in a one-on-one setting where a tutor is working with only one student at a time. In this case, the tutor would scaffold the push and support cards as appropriate for the learner.
A Note About Notice/Wonder
All of the tasks within or linked to in this curriculum guide have been adapted for the multi-level adult education classroom by removing any questions that appeared on the first page of the original task and replacing the question(s) with notice/wonder. Removing the original question(s) serves multiple purposes.
For one, it acts to slow students down so that they do not immediately jump into calculations before they actually understand the information that is being presented. In addition, it gives students opportunity to express some of the math ideas that are already in their head and to verbalize something they are pondering but might not have the courage to say out loud unless everyone else is in the game. There is no pressure here to immediately come up with an answer, so students who have not yet developed confidence in their math problem-solving skills can freely participate. A more detailed, step-by-step guide on how to implement this powerful classroom strategy in your classroom can be found in OER Commons. [4]

Ever Wonder What They'd Notice? (if only someone would ask)
A well invested five minutes: To catch the excitement of how notice/wonder helps to draw out the mathematical thinking of our students, please follow this link to watch the video: Ever Wonder What They’d Notice? (if only someone would ask).
The Student Centered Classroom Routine
Some of the tasks that are recommended in this curriculum guide already contain sufficient guidance for use in the classroom as is. As for the tasks lacking this, what follows is a suggested framework. Consider how you can formatively assess your students during each step.
- Give students the notice/wonder page of the activity and ask them to silently work on this for 3 - 5 minutes. This gives students time to draw up any background information they already have about the situation or visual model. Float about the room and look for some varied responses. Quietly ask a few of the students, whose thinking you would like to draw out during the whole group discussion, if they would mind sharing their thinking with the whole group. This prepares them to think about how they want to express themselves.
- After quiet time, have students share out what they notice and record their responses. This is a time when some students may notice some math vocabulary or concepts that are either essential to understand the problem, or may be something you know will show up on a high-stakes exam. If a student mentions something, for example the word vertices, ask the student to elaborate: “Could you talk a little more about that?
- Share out what students wonder and record their responses. If their wonderings are vague, ask them to elaborate.
- Be sure to include wait time in both asking what students notice and what they wonder. This may seem a bit of an awkward silence if you are not used to wait time, but it’s essential to give all students the opportunity to participate, as some students are slow to raise their hand. Did you see anything unique, funny, or witty on a student’s paper that wasn’t mentioned yet? Perhaps that student is ready to share out now.
- Once students have shared out all of their observations and questions, the initial task can be given to students. Many times, the actual question (or a form of the question or task) that you want students to focus on, actually comes from the students, themselves, during notice/wonder. Be sure to make that connection as this invests students in the task: they own it. Give students 3 - 5 minutes of quiet time to individually work on the initial task.
- Now it’s time to break out the push and support cards! (See: How to Use Push and Support in Your Classroom.)
- As students are working through the problem, making use of the push and support cards, note the diverse problem solving strategies that students use while solving the task. Remember: not all students (or groups) may have gotten to the same level during the activity. Some students may have focused on concrete representations in the form of pictures or manipulatives, others may have used guess & check, some may have used a way to organize their information (a number line, diagram, or a function table), while others may have extended the problem to abstract procedures. Note at least three different ways students (or groups of students) worked with the problem. You may want to ask students ahead of time to share their discoveries when the whole group comes together to discuss the task.
- Share out. There are different ways that you may choose to have students share out their discoveries. Below are two suggestions:
- (1) Ask each group to create a poster that illustrates what they discovered and depicts the strategies they used in their exploration of the problem. The group should elect a spokesperson who will present their project to the class. The rest of the class should be encouraged to ask questions of the group when the spokesperson is finished presenting.
- (2 ) Ask individual students to share out, one-at-a time, the way he or she approached the problem, sequencing the presenting of the strategies from the concrete to the more abstract. You may choose to have the student recreate the strategy on chart paper or the board, or the student may stay seated and describe the strategy, step-by-step, whilst you recreate it on the board or chart paper. As with option (1), the whole class should be asked if they have any questions for the student who shared his or her thinking.
Whichever share-out method you choose, it is best to have them displayed side-by-side so that students can compare the strategies as a whole group. How are they the same? How are they different? The point here is for students to develop flexibility when working with problems, learn new problem solving strategies, and understand the connections between the different strategies.
Download and print: The Student-Centered Classroom Routine
Tasks
Download and print all tasks: Tasks
| Activity Name | CCRSAE Alignment (Corresponds to CCSS Alignment) |
| The Freeway | Use units as a way to understand problems and to guide the solutions of multi-step problems. (N.Q.1) Choose a level of accuracy appropriate to limitations on measurement when reporting quantities. (N.Q.3) |
| Analyze and solve linear equations and pairs of simultaneous linear equations. (8.EE.7) (8.EE.8) | |
| Solve systems of linear equations exactly and approximately, focusing on pairs of linear equations with two variables. (A.REI.6) | |
| Saving for Mom’s Present * |
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters. (A.REI.3) Represent and solve equations and inequalities graphically. (A.REI.10) |
| The Paycheck Problem* |
Understand the concept of a function and use function notation. (F.IF.2) Interpret functions that arise in applications in terms of the context. (F.IF.4) |
| The Painted Cube* | Distinguish between situations that can be modeled with linear functions and with exponential functions. (F.LE.1) Reason abstractly and quantitatively (MP 2) Look for and express regularity in repeated reasoning. (MP 8) |
| Bacteria Population Growth Lesson Plan*
|
Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases. (F.IF.7) Use properties of exponents to interpret expressions for exponential functions. (F.IF.8b) |
*Examples of student work are available by accessing the Google Doc.
Reflection Activity
If you have been using the tasks linked to in this curriculum guide, now would be a good time to examine what some of the problems looked like before they were adapted for the multi-level adult education classroom and before the push and support cards were added to the tasks. This will give you some ideas on how you can modify the many rich tasks that already exist at OER Commons. Examine at least one of the problems listed below in its original form, designed for use in Grades 8-12, and then compare that with the repurposed version, designed for ABE/HSE adult education students. It is recommended that you complete this reflection activity before moving on to the next section.
Original Form at OER Commons (Select Student View) | Repurposed for Adult Education |
| What did you notice? | What did you wonder? |
How to Create Push and Support Cards Using OER Commons Resources
After your examination of both the original problems and the repurposed version of the of problems, you most likely have a lot of ideas now about how to create push and support cards. Keep in mind that the cards should be designed to encourage mathematical thinking as described in The Standards for Mathematical Practice. [2]
Here are a few suggestions on how to get started writing push and support cards:
- Remove all questions and replace with notice/wonder
- Suggest the use of manipulatives
- Suggest students draw a picture to model the situation
- Suggest students organize their information
- Suggest students plug simpler numbers into the problem
- Provide a function table with some of the information filled in
- Use questions from original problem as push cards
- Ask students if they see a pattern
- Ask students to write a similar problem
- Ask “What if?” questions
- Ask “Is it possible?” questions
- Provide challenges where students have to work backwards, such as solving for x
For some additional support regarding the de-evolution of a math problem, so as to include push and support, see the Math Memos write up about The Paycheck Problem.
Conclusion
While the focus of this curriculum guide has been on how to implement the strategy of push and support cards in your classroom, it is evident that there are additional factors that contribute to ensuring that these cards are used as an effective differentiation tool. The cards should be connected to an open-ended non-routine problem that all learners in a multi-level class can find a way in to, and then scaffold up to a level that is individually appropriate. Every student needs to be afforded time to allow their own thinking to emerge, and then given the opportunity to collaborate with other students, so they can hear their own voice, have their own voice, and value their own voice in the math classroom.
This means that there needs to be a relationship built between teacher and students where it is understood that the teacher is not the keeper of all knowledge. Rather, conceptual understanding of mathematics and a productive disposition that fuels problem solving happens in the students’ minds and in their conversations when they question each other, explain their problem solving strategies, and rely on group conversations to confirm the solution to a math problem. Notice/wonder, high-cognitive tasks, think time, push and support cards, and collaboration are a few strategies that can be utilized to foster this kind of learning environment where all students in a multi-level classroom can become masters of their own learning.
References
[1] Curry, D. (2017). Using the PIAAC Numeracy Framework to Guide Instruction: An Introduction for Adult Educators. Retrieved May 04, 2018, from https://bit.ly/2qRLC1J. Washington, DC.
[2] Common Core State Standards Initiative, Standards for Mathematical Practice, 2018. Retrieved May 10, 2018 from http://www.corestandards.org/Math/Practice/
[3] Appleton, Eric (2017). A Strategy for Teaching in a Multi-Level Classroom: Push and Support Cards, The MATH Practitioner, Volume 22, Issue 3, Summer 2017. Retrieved May 04, 2017 from https://bit.ly/2rm6Tzi.
[4] OER Commons, Trushkowsky M. (2016) What Do You Notice? What Do You Wonder? Retrieved May 11, 2018 from https://www.oercommons.org/courses/what-do-you-notice-what-do-you-wonder
[5] OER Commons,Illustrative Mathematics, (2016). Felicia’s Drive. Retrieved May 10, 2018 from https://www.oercommons.org/courses/felicia-s-drive
[6] OER Commons, Illustrative Mathematics, (2016). Fixing the Furnace. Retrieved May 10, 2018 from https://www.oercommons.org/courses/fixing-the-furnace
[7] OER Commons, Illustrative Mathematics, (2016). Accurately weighing pennies I. Retrieved May 10, 2018 from https://www.oercommons.org/courses/accurately-weighing-pennies-i
[8] OER Commons, Appleton, E. (2015). A Window into International Education and Problem Solving in the Mathematics Classroom. Retrieved May 11, 2018 from https://www.oercommons.org/courses/a-window-into-international-education-and-problem-solving-in-the-mathematics-classroom