Exploring Ratios and Proportions: 6.RP.3

Solving Proportions: 6.RP.3

Warm up:  “What do you notice...,  what do you wonder?”

Using fraction strips, have students discuss patterns and relationships, and then predict the next table shading... 

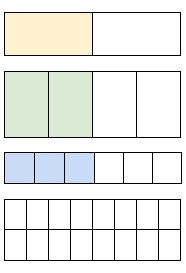
There are 4 different sized rectangles. All rectangles are different sizes. The first rectangle is cut into 2 equal parts (one row of 4), one of which is yellow. The second rectangle is cut into 4 equal parts, 2 of which are green. The third rectangle is cut into 6 equal parts, 3 of which are blue. The last rectangle is cut into 16 equal parts (2 rows of 8) without any shading.

Having student explore and discuss patterns and relationships they see, as well as predict the shading of the next rectangle will help them demonstrate any prior knowledge. Depending on internet access, this can either be printed,  projected, or on a smartboard.

Introduction/Review:

Intro/Review of Ratios:

Khan Academy Video:  Intro to Ratios  

This Khan Academy video could be either an introduction or review for equivalent ratios, depending on the student’s background knowledge.

Solving Proportions

Khan Academy:   Solving Proportions

This Khan Academy lesson walks through how to set up and solve a proportion.  Both of these videos are connected to practice problems, for students at varying levels to get 

Application/formative assessment:

Nana Paint Mix-up

This is where the student can practice setting up a proportion in a “real life” situation.  These are like authentic story problems that students have to determine the important data, find relationships, determine what needs to be solved, and solve it.  Having students justify their reasoning, as well as explain their problem solving process will be a great formative assessment of how much the students understand.

Practice and summative assessment

Algebra by Example

3.4  Writing Proportions

3.5  Solving Proportions         

Under: Linear Equations in Algebra by Example, look at sections 3.4, 3.5

Although they may need additional practice to fully develop fluency, these sheets help the students demonstrate their understanding. Students start by examining other “student work”. If there is an error, they have to determine the  mathematical errors they made. If there is not an error, they explain the reasoning in the steps, to show deeper understanding.  Their level of understanding will be evident in their explanation of the other students work.  The student is also asked complete similar problems, to show their understanding.  Answer keys are available.