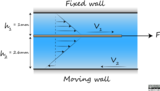
Fluid Mechanics problems for the WeBWorK open online homework system. Includes problems from second-year level.

The "tested" problems have been deployed in a class. The "untested" problems have been tested by the creators, but not yet deployed in a class.

These problems need to be uploaded into an instance of WeBWorK to use/assign them.

Students learn about water poverty and how water engineers can develop appropriate solutions to a problem that is plaguing nearly a sixth of the world's population. Students follow the engineering design process to design a gravity-fed water system. They choose between different system parameters such as pipe sizes, elevation differentials between entry and exit pipes, pipe lengths and tube locations to find a design that provides the maximum flow and minimum water turbidity (cloudiness) at the point of use. In this activity, students play the role of water engineers by designing and building model gravity-fed water systems, learning the key elements necessary for viable projects that help improve the lives people in developing communities.

This course covers the development of the fundamental equations of fluid mechanics and their simplifications for several areas of marine hydrodynamics and the application of these principles to the solution of engineering problems. Topics include the principles of conservation of mass, momentum and energy, lift and drag forces, laminar and turbulent flows, dimensional analysis, added mass, and linear surface waves, including wave velocities, propagation phenomena, and descriptions of real sea waves. Wave forces on structures are treated in the context of design and basic seakeeping analysis of ships and offshore platforms. Geophysical fluid dynamics will also be addressed including distributions of salinity, temperature, and density; heat balance in the ocean; major ocean circulations and geostrophic flows; and the influence of wind stress. Experimental projects conducted in ocean engineering laboratories illustrating concepts taught in class, including ship resistance and model testing, lift and drag forces on submerged bodies, and vehicle propulsion.

Student teams design, build and test small-sized gliders to maximize flight distance and an aerodynamic ratio, applying their knowledge of fluid dynamics to its role in flight. Students experience the entire engineering design process, from brainstorming to CAD (or by hand) drafting, including researching (physics of aerodynamics and glider components that take advantage of that science), creating materials lists, constructing, testing and evaluating—all within constraints (works with a launcher, budget limitation, maximizing flight distance to mass ratio), and concluding with a summary final report. Numerous handouts and rubrics are provided.

This course emphasizes concepts and techniques for solving integral equations from an applied mathematics perspective. Material is selected from the following topics: Volterra and Fredholm equations, Fredholm theory, the Hilbert-Schmidt theorem; Wiener-Hopf Method; Wiener-Hopf Method and partial differential equations; the Hilbert Problem and singular integral equations of Cauchy type; inverse scattering transform; and group theory. Examples are taken from fluid and solid mechanics, acoustics, quantum mechanics, and other applications.

This is an open-source graduate level textbook covering the fundamentals of incompressible fluid flow. The topics cover the derivation of conservation mass, momentum, and energy equations, kinematics of fluid motion, non-dimensionalization and order-of-magnitude analysis, Stokes flows, potential flows, and boundary layers. The textbook was developed for a graduate level course at the Colorado School of Mines Department of Mechanical Engineering. We try to build from the typical math proficiency of incoming grad students, many of whom have never taken a course in PDEs, and may not be comfortable with vector operations such as the gradient, divergence, and Laplacian. Please feel free to contact Nils Tilton at ntilton@mines for any suggested revisions. We can share the latex files as well if you wish to modify the textbook for your own purposes.

This lab activity allows students to apply their knowledge of Archimedes' Principle by calculating the maximum buoyant force that a ship can produce.

This activity is a lab where students design an experiment to construct a self-powered mini-submarine that stays underwater for at least 10 seconds, and then float back up to the top of the water level. Buoyancy and density are applied and discussed.

These videos were created in 2017 to support an online version of the first course in Fluid Mechanics in the Department of Mechanical and Materials Engineering at Queen's University at Kingston, Ontario, Canada. They comprise the content equivalent of a full course of lectures and assume a textbook as a backup resource.

Students calculate the viscosity of various household fluids by measuring the amount of time it takes marble or steel balls to fall given distances through the liquids. They experience what viscosity means, and also practice using algebra and unit conversions.

This course is an advanced subject in fluid and continuum mechanics. The course content includes kinematics, macroscopic balances for linear and angular momentum, stress tensors, creeping flows and the lubrication approximation, the boundary layer approximation, linear stability theory, and some simple turbulent flows.

Modelling is about understanding the nature: our world, ourselves and our work. Everything that we observe has a cause (typically several) and has the effect thereof. The heart of modelling lies in identifying, understanding and quantifying these cause-and-effect relationships.

A model can be treated as a (selective) representation of a system. We create the model by defining a mapping from the system space to the model space, thus we can map system state and behaviour to model state and behaviour. By defining the inverse mapping, we may map results from the study of the model back to the system. In this course, using an overarching modelling paradigm, students will become familiar with several instances of modelling, e.g., mechanics, thermal dynamics, fluid mechanics, etc.

Continuation of Physics 1. Topics include: simple harmonic motion, gravitation, fluid mechanics, waves, the kinetic theory of gases, and the first and second laws of thermodynamics. This course is a calculus-based physics course that is required by four-year colleges in science and engineering studies.

8.01L is an introductory mechanics course, which covers all the topics covered in 8.01T. The class meets throughout the fall, and continues throughout the Independent Activities Period (IAP).

From drinking fountains at playgrounds, water systems in homes, and working bathrooms at schools to hydraulic bridges and levee systems, fluid mechanics are an essential part of daily life. Fluid mechanics, the study of how forces are applied to fluids, is outlined in this unit as a sequence of two lessons and three corresponding activities. The first lesson provides a basic introduction to Pascal's law, Archimedes' principle and Bernoulli's principle and presents fundamental definitions, equations and problems to solve with students, as well as engineering applications. The second lesson provides a basic introduction to above-ground storage tanks, their pervasive use in the Houston Ship Channel, and different types of storage tank failure in major storms and hurricanes. The unit concludes with students applying what they have learned to determine the stability of individual above-ground storage tanks given specific storm conditions so they can analyze their stability in changing storm conditions, followed by a project to design their own storage tanks to address the issues of uplift, displacement and buckling in storm conditions.

Students are presented with a challenge question that they must answer with scientific and mathematical reasoning. The challenge question is: "You have a large rock on a boat that is floating in a pond. You throw the rock overboard and it sinks to the bottom of the pond. Does the water level in the pond rise, drop or remain the same?" Students observe Archimedes' principle in action in this model recreation of the challenge question when a toy boat is placed in a container of water and a rock is placed on the floating boat. Students use terminology learned in the classroom as well as critical thinking skills to derive equations needed to answer this question.

Students use their understanding of projectile physics and fluid dynamics to find the water pressure in water guns. By measuring the range of the water jets, they are able to calculate the theoretical pressure. Students create graphs to analyze how the predicted pressure relates to the number of times they pump the water gun before shooting.