Using CSS to change size of items.
- Subject:
- Applied Science
- Computer Science
- Material Type:
- Interactive
- Lesson
- Provider:
- Khan Academy
- Provider Set:
- Khan Academy
- Author:
- Pamela Fox
- Date Added:
- 07/11/2021

Using CSS to change size of items.
Julius Caesar installs Cleopatra as Pharaoh in Ptolemaic Egypt and becomes Dictator for Life, only to be assassinated by Brutus on the Ides of March.
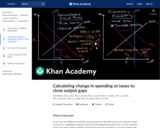
Recall that the tax multiplier and expenditure multiplier magnify the effect of any change in spending or taxes. In this video, we use that fact to calculate the amount of spending or tax change necessary to close output gaps.
Calculating the dot and cross products when vectors are presented in their x, y, and z (or i, j, and k) components. Created by Sal Khan.
In this video we take a slightly different approach to understanding the difference between real and nominal values: find the value of an asset in a previous year's dollars. Created by Sal Khan.
An overview of calculating results with CASE
How to calculate state taxes and take-home pay.Created by Sal Khan.
This series of videos focusing on calculus covers sample questions from the A.P, Calculus AB and AC exams (both multiple choice and free answer).
The Calculus BC AP exam is a super set of the AB exam. It covers everything in AB as well as some of the more advanced topics in integration, sequences and function approximation. This tutorial is great practice for anyone looking to test their calculus mettle!
This series of videos focusing on calculus covers minima, maxima, and critical points, rates of change, optimization, rates of change, L'Hopital's Rule, mean value theorem.
A single definite integral can be used to find the area under a curve. with double integrals, we can start thinking about the volume under a surface!
This is about as many integrals we can use before our brains explode. Now we can sum variable quantities in three-dimensions (what is the mass of a 3-D wacky object that has variable mass)!
This series of videos focusing on calculus covers indefinite integral as anti-derivative, definite integral as area under a curve, integration by parts, u-substitution, trig substitution.
This 9-minute video lesson provides an introduction to L'Hopital's Rule. [Calculus playlist: Lesson 36 of 156]
This series of videos focusing on calculus covers limit introduction, squeeze theorem, and epsilon-delta definition of limits.
Limits are the core tool that we build upon for calculus. Many times, a function can be undefined at a point, but we can think about what the function "approaches" as it gets closer and closer to that point (this is the "limit"). Other times, the function may be defined at a point, but it may approach a different limit. There are many, many times where the function value is the same as the limit at a point. Either way, this is a powerful tool as we start thinking about slope of a tangent line to a curve.
This tutorial covers much of the same material as the "Limits" tutorial, but does it with Sal's original "old school" videos. The sound, resolution or handwriting isn't as good, but some people find them more charming.
This series of videos focusing on calculus covers line integral of scalar and vector-valued functions, Green's Theorem and 2-D Divergence Teorem.
It is sometimes easier to take a double integral (a particular double integral as we'll see) over a region and sometimes easier to take a line integral around the boundary. Green's theorem draws the connection between the two so we can go back and forth. This tutorial proves Green's theorem and then gives a few examples of using it. If you can take line integrals through vector fields, you're ready for Mr. Green.
With traditional integrals, our "path" was straight and linear (most of the time, we traversed the x-axis). Now we can explore taking integrals over any line or curve (called line integrals).